Question

4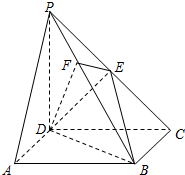．如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F．
（Ⅰ）求证：DE⊥平面PBC；
（Ⅱ）求二面角F-DE-B的正弦值．

Answer 1

分析 （Ⅰ）建立空间直角坐标系，点D为坐标原点，设DC=1．求出相关点的坐标，利用数量积为0，证明BC⊥DE．PC⊥DE，即可证明DE⊥平面PBC．
（Ⅱ）求出平面EFD的一个法向量，平面DEB的法向量，设求二面角F-DE-B的平面角为θ，利用空间向量的数量积求解即可．

解答 （Ⅰ）∵侧棱PD⊥底面ABCD，底面ABCD是正方形，
∴如图建立空间直角坐标系，点D为坐标原点，设DC=1．
依题意得$A（1，0，0），P（0，0，1），E（0，\frac{1}{2}，\frac{1}{2}）$．B（1，1，0），C（0，1，0）
$\overrightarrow{DE}=（0，\frac{1}{2}，\frac{1}{2}）$，$\overrightarrow{BC}=（-1，0，0）$$\overrightarrow{PC}=（0，1，-1）$
故$\overrightarrow{BC}•\overrightarrow{DE}=0$，$\overrightarrow{PC}•\overrightarrow{DE}=0$
所以BC⊥DE．PC⊥DE
∵PC∩BC=C
∴DE⊥平面PBC
（Ⅱ）$B（1，1，0），\overrightarrow{PB}=（1，1，-1）$，又$\overrightarrow{DE}=（0，\frac{1}{2}，\frac{1}{2}）$，故$\overrightarrow{PB}•\overrightarrow{DE}=0$，所以PB⊥DE．
由已知EF⊥PB，且EF∩DE=E，所以PB⊥平面EFD．
所以平面EFD的一个法向量为$\overrightarrow{PB}=（1，1，-1）$.$\overrightarrow{DE}=（0，\frac{1}{2}，\frac{1}{2}），\overrightarrow{DB}=（1，1，0）$，
不妨设平面DEB的法向量为$\overrightarrow a=（x，y，z）$
则$\left\{\begin{array}{l}\overrightarrow a•\overrightarrow{DE}=\frac{1}{2}（y+z）=0\\ \overrightarrow a•\overrightarrow{DB}=x+y=0\end{array}\right.$

不妨取x=1则y=-1，z=1，
即$\overrightarrow a=（1，-1，1）$…（10分）
设求二面角F-DE-B的平面角为θ，
$cosθ=\frac{{\overrightarrow a•\overrightarrow{PB}}}{{|\overrightarrow a||\overrightarrow{PB}|}}=-\frac{1}{3}$…（11分）
因为θ∈[0，π]，所以$sinθ=\frac{{2\sqrt{2}}}{3}$．
二面角F-DE-B的正弦值大小为$\frac{{2\sqrt{2}}}{3}$．

点评 本题考查二面角的平面角的求法，空间向量数量积的应用，考查计算能力，转化思想的应用．