题目内容
1．
如图所示，在正方形纸片ABCD中，AC与BD相交于点O，剪去△AOB，将剩余部分沿OC、OD折叠，使OA、OB重合，则在以A（B）、C、D、O为顶点的四面体中，二面角O-AD-C的余弦值为（ ）| A． | $\frac{\sqrt{6}}{5}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{5}}{3}$ | D． | $\frac{\sqrt{6}}{3}$ |
分析 根据题意，求出翻折后的几何体为底面边长，侧棱长，高，即可求出棱锥的体积．
解答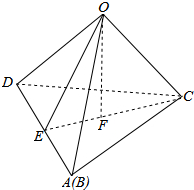 
解：设正方形纸片ABCD的边长为4，则翻折后的几何体为底面边长为4，侧棱长为2$\sqrt{2}$的正三棱锥，如图：作CE⊥AD于E，E为AD的中点，则OE⊥AD，∠OEC就是二面角O-AD-C的平面角，
OE=$\sqrt{（2\sqrt{2}）^{2}-{2}^{2}}$=2，CE=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$，CO=2$\sqrt{2}$．
可得OE⊥OC，
cos∠OEC=$\frac{OE}{CE}$=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$．
故选：B．
点评 本题考查几何体的二面角的求法，折叠问题的处理方法，找出二面角的平面角是解题的关键，考查计算能力，是中档题．
练习册系列答案
相关题目