题目内容
已知定义在R上的函数f(x)=
x3+
(a-4)x2+2(2-a)x+a的图象与y轴的交点和原点的距离小于或等于1.
(1)求实数a的取值范围;
(2)是否存在这样的区间,对任意的a的可能取值,函数f(x)在该区间上都是单调递增的?若存在,则求出这样的区间,若不存在,则说明理由.
| 1 |
| 3 |
| 1 |
| 2 |
(1)求实数a的取值范围;
(2)是否存在这样的区间,对任意的a的可能取值,函数f(x)在该区间上都是单调递增的?若存在,则求出这样的区间,若不存在,则说明理由.
考点:利用导数研究函数的单调性
专题:函数的性质及应用,导数的综合应用
分析:(1)函数图象与y轴交点为(0,a),则|a|≤1,从而可求
(2)对函数求导,由函数f(x)在该区间上为增函数可得f'(x)>0对任意的a∈[-1,1]恒成立,构造关于a的函数g(a)=(x-2)a+x2-4x+4>0对任意的a∈[-1,1]恒成,结合一次函数的性质可求x的范围
(2)对函数求导,由函数f(x)在该区间上为增函数可得f'(x)>0对任意的a∈[-1,1]恒成立,构造关于a的函数g(a)=(x-2)a+x2-4x+4>0对任意的a∈[-1,1]恒成,结合一次函数的性质可求x的范围
解答:
解:(1)函数图象与y轴交点为(0,a),则|a|≤1,∴-1≤a≤1;
(2)f'(x)=x2+(a-4)x+2(2-a)=(x-2)a+x2-4x+4,
令f'(x)>0对任意的a∈[-1,1]恒成立,
即不等式g(a)=(x-2)a+x2-4x+4>0对任意的a∈[-1,1]恒成立,
其充要条件是:
,解得x<1,或x>3.
所以当x∈(-∞,1)或x∈(3,+∞)时,f'(x)>0对任意a∈[-1,1]恒成立,
所以对任意a∈[-1,1]函数f(x)均是单调增函数.
故存在区间(-∞,1)和(3,+∞),对任意a∈[-1,1],f(x)在该区间内均是单调增函数.
(2)f'(x)=x2+(a-4)x+2(2-a)=(x-2)a+x2-4x+4,
令f'(x)>0对任意的a∈[-1,1]恒成立,
即不等式g(a)=(x-2)a+x2-4x+4>0对任意的a∈[-1,1]恒成立,
其充要条件是:
|
所以当x∈(-∞,1)或x∈(3,+∞)时,f'(x)>0对任意a∈[-1,1]恒成立,
所以对任意a∈[-1,1]函数f(x)均是单调增函数.
故存在区间(-∞,1)和(3,+∞),对任意a∈[-1,1],f(x)在该区间内均是单调增函数.
点评:本题主要考查了利用导数与函数 的单调性的关系的应用,解题的关键是根据导数的知识得到f'(x)>0对任意的a∈[-1,1]恒成立时,构造关于a的一次函数进行求解,体现了转化的思想在解题中的应用.

练习册系列答案
相关题目
 如图,?ABCD中,点M是AB的中点,CM与BD相交于点N,若
如图,?ABCD中,点M是AB的中点,CM与BD相交于点N,若
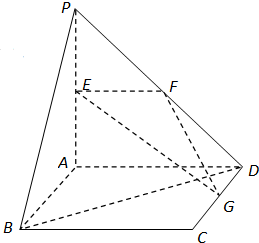 如图,直线PA⊥平面ABCD,四边形ABCD是正方形,且PA=AD=2,点E、F、G分别是线段PA、PD、CD的中点.
如图,直线PA⊥平面ABCD,四边形ABCD是正方形,且PA=AD=2,点E、F、G分别是线段PA、PD、CD的中点.