题目内容
四棱柱ABCD-A1B1C1D1的三视图和直观图如下:
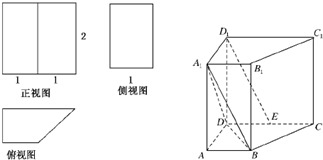
(1)求出该四棱柱的表面积;
(2)设E是DC上一点,试确定E的位置,使D1E∥平面A1BD,并说明理由.

(1)求出该四棱柱的表面积;
(2)设E是DC上一点,试确定E的位置,使D1E∥平面A1BD,并说明理由.
考点:棱柱、棱锥、棱台的侧面积和表面积,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)利用四棱柱的表面积公式,即可得出结论;
(2)确定E的位置,使D1E∥平面A1BD,设AD1∩A1D=M,BD∩AE=N,连接MN,证明MN∥D1E即可.
(2)确定E的位置,使D1E∥平面A1BD,设AD1∩A1D=M,BD∩AE=N,连接MN,证明MN∥D1E即可.
解答:
解:(1)由已知数据可知,四棱柱的表面积
S=2×1+2×1+2×2+2×
×1+2×
=11+2
;
(2)连接AD1、AE,设AD1∩A1D=M,BD∩AE=N,连接MN,如图所示.
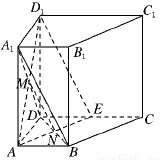
∵平面AD1E∩平面A1BD=MN,
要使D1E∥平面A1BD,需使MN∥D1E,
又M是AD1的中点,∴N是AE的中点.
又△ABN≌△EDN,
∴AB=DE.
即E是DC的中点.
综上所述,当E是DC的中点时,可使D1E∥平面A1BD.
S=2×1+2×1+2×2+2×
| 1+2 |
| 2 |
| 2 |
| 2 |
(2)连接AD1、AE,设AD1∩A1D=M,BD∩AE=N,连接MN,如图所示.

∵平面AD1E∩平面A1BD=MN,
要使D1E∥平面A1BD,需使MN∥D1E,
又M是AD1的中点,∴N是AE的中点.
又△ABN≌△EDN,
∴AB=DE.
即E是DC的中点.
综上所述,当E是DC的中点时,可使D1E∥平面A1BD.
点评:本题考查直线与平面的平行,空间中直线与平面的位置关系,是中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
用1,2,3,4,5,6,7七个数字排列组成七位数,使其中偶位数上必定是偶数,那么可得七位数的个数是( )
| A、A44 |
| B、A44A33 |
| C、6A33 |
| D、C152C403A55 |