题目内容
13. 在△ABC中,∠C是锐角,且满足$\sqrt{3}$a2-$\sqrt{3}$b2=2c2sin(A-B).
在△ABC中,∠C是锐角,且满足$\sqrt{3}$a2-$\sqrt{3}$b2=2c2sin(A-B).(1)求角C;
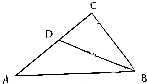
(2)若c=1,且AC边上的中线BD长为$\frac{\sqrt{3}}{3}$,求△ABC的面积.
分析 (1)使用正弦定理将边化角,使用和差化积公式化简即可得出sinC;
(2)分别在△ABC和△BCD中使用余弦定理,解方程组得出BC,CD,代入面积公式计算面积.
解答 解:(1)在△ABC中,∵$\sqrt{3}$a2-$\sqrt{3}$b2=2c2sin(A-B),
∴$\sqrt{3}$(sin2A-sin2B)=2sin2Csin(A-B).
∴$\sqrt{3}$(sinA+sinB)(sinA-sinB)=2sin2Csin(A-B).
∴$\sqrt{3}$•2sin$\frac{A+B}{2}$cos$\frac{A-B}{2}$•2cos$\frac{A+B}{2}$sin$\frac{A-B}{2}$=2sin2Csin(A-B).
∴$\sqrt{3}$sin(A+B)sin(A-B)=2sin2Csin(A-B).
∴sinC=$\frac{\sqrt{3}}{2}$.
∵C是锐角,∴C=$\frac{π}{3}$.
(2)设CD=AD=x,BC=y,
在△ABC中,由余弦定理得1=4x2+y2-2xy,
在△BCD中,由余弦定理得$\frac{1}{3}$=x2+y2-xy.
联立方程组$\left\{\begin{array}{l}{4{x}^{2}+{y}^{2}-2xy=1}\\{{x}^{2}+{y}^{2}-xy=\frac{1}{3}}\end{array}\right.$,解得x=y=$\frac{\sqrt{3}}{3}$.即AC=$\frac{2\sqrt{3}}{3}$,BC=$\frac{\sqrt{3}}{3}$.
∴S△ABC=$\frac{1}{2}AC•BCsinC$=$\frac{1}{2}×\frac{2\sqrt{3}}{3}×\frac{\sqrt{3}}{3}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{6}$.
点评 本题考查了正弦定理,余弦定理,三角函数的恒等变换,属于中档题.

 通城学典默写能手系列答案
通城学典默写能手系列答案| A. | {0,1} | B. | {-1,1} | C. | {-1,0} | D. | {-1,0,1} |
| A. | $\frac{1}{7}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{9}$ |
| A. | an=$\sqrt{n+1}$-$\sqrt{n}$ | B. | an=$\sqrt{n}$-$\sqrt{n-1}$ | C. | an=$\sqrt{n+2}$-$\sqrt{n+1}$ | D. | an=2$\sqrt{n}$-1 |
| A. | [1,5] | B. | [2,5] | C. | [-2,2] | D. | [5,9] |
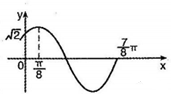 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则此函数的解析式为f(x)=2sin(2x+$\frac{π}{4}$).
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则此函数的解析式为f(x)=2sin(2x+$\frac{π}{4}$).