题目内容
1.已知定义在R上的函数f(x)满足f(-x)=-f(x),f(2-x)=f(x),当x∈(0,1]时,f(x)=$\frac{1}{x-2}$.(1)当x∈[1,2)时,求f(x)的解析式;
(2)计算f(0)+f(1)+f(2)+…+f(2016)的值.
分析 (1)根据函数的关系,利用转化法进行求解即可.
(2)根据函数的周期性进行求出,求出函数在一个周期内的函数值之和即可.
解答 解:(1)由f(-x)=-f(x),得函数为奇函数,
∵f(2-x)=f(x)=-f(x-2),
∴f(x+2)=-f(x),即f(x+4)=-f(x+2)=f(x),则函数的周期是4,
当x∈[1,2)时,当-x∈(-2,-1],2-x∈(0,1],
∵当x∈(0,1]时,f(x)=$\frac{1}{x-2}$.
∴当x∈[1,2)时,f(x)=f(2-x)=$\frac{1}{2-x-2}$=-$\frac{1}{x}$.
(2)∵f(x)是定义在R上的奇函数,∴f(0)=0,
f(1)=-1,f(2)=f(0)=0,f(3)=f(3-4)=f(-1)=-f(1)=1,
则f(0)+f(1)+f(2)+f(4)=0-1+0+1=0,
则f(0)+f(1)+f(2)+…+f(2016)=504×[f(1)+f(2)+f(3)+f(4)]+f(0)=0
点评 本题主要考查函数解析式的求解以及函数值的计算,根据条件判断函数的周期性和对称性是解决本题的关键.

练习册系列答案
相关题目
11.设α、β是两个不同的平面,b是直线且b?β,“b⊥α”是“α⊥β”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.在一次抽样活动中,采取系统抽样的方法,若第一组抽取的是2号,第二组抽取的是12号,则第三组抽取的是( )
| A. | 21号 | B. | 22号 | C. | 23号 | D. | 24号 |
9.其几何体的三视图如图所示(其中俯视图中的圆弧是半圆),则该几何体的表面积为( )
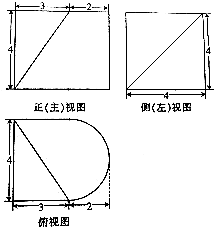

| A. | 44+2$\sqrt{34}$+8π | B. | 56+8π | C. | 44+2$\sqrt{34}$+12π | D. | 56+12π |
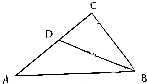 在△ABC中,∠C是锐角,且满足$\sqrt{3}$a2-$\sqrt{3}$b2=2c2sin(A-B).
在△ABC中,∠C是锐角,且满足$\sqrt{3}$a2-$\sqrt{3}$b2=2c2sin(A-B).