题目内容
19.若椭圆$\frac{x^2}{25}+\frac{y^2}{m}$=1与双曲线x2-15y2=15的焦距相等,则m的值为9或41.分析 先将双曲线的方程化为标准方程,求出双曲线和椭圆的焦距,即可得出结论.
解答 解:双曲线x2-15y2=15即为:$\frac{{x}^{2}}{15}$-y2=1,c2=a2+b2=15+1=16,c=4,
焦点为(±4,0),
椭圆$\frac{x^2}{25}+\frac{y^2}{m}$=1的a′=5,b′=$\sqrt{m}$,c′=4,或a′=$\sqrt{m}$,b′=5,c′=4
∴25=m+16,或m=25+16,
∴m=9或41.
故答案为:9或41.
点评 本题考查椭圆和双曲线的方程和性质,注意它们的区别,考查运算能力,属于基础题.

练习册系列答案
相关题目
8.为了了解某地区20000个家庭日常用水情况,采用抽样调查的方式,通过分析样本数据来估计整个地区居民用水量的分布情况.假设通过抽样,获得了100个家庭(单位:户)某年的月平均用水量(单位:吨),整理数据后制成如下频数分布表:
根据以上表格
(1)估计本地区居民月均用水量的众数,中位数,平均数.
(2)估计本地区居民月均用水量在(1.1,2.8)间的户数.
| 分组 | [0,0.5) | [0.5,1) | [1,1.5) | [1.5,2) | [2,1.5) | [2.5,3) | [3,3.5) | [3.5,4) | [4,4.5) |
| 频数 | 4 | 8 | 15 | 22 | 25 | 14 | 6 | 4 | 2 |
(1)估计本地区居民月均用水量的众数,中位数,平均数.
(2)估计本地区居民月均用水量在(1.1,2.8)间的户数.
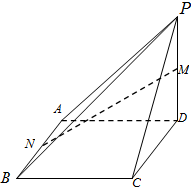 如图:在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=DA=DC=2.
如图:在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=DA=DC=2.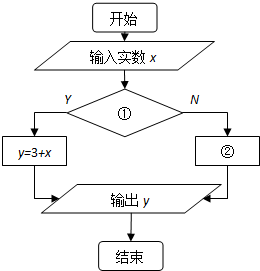 已知函数y=|x+3|,向量程序框表示的是给出x值,求所对应的函数值的算法,请将该程序框图补充完整,其中①处应填x≥-3;②处应填y=-x-3.
已知函数y=|x+3|,向量程序框表示的是给出x值,求所对应的函数值的算法,请将该程序框图补充完整,其中①处应填x≥-3;②处应填y=-x-3.