题目内容
14.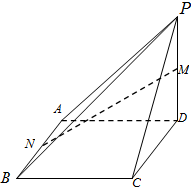 如图:在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=DA=DC=2.
如图:在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=DA=DC=2.(1)若M、N分别是PD、AB的中点,证明:MN∥平面PBC;
(2)求二面角C-BP-D的大小.
分析 (1)欲证MN∥平面PBC,根据MN?平面MNE,可先证平面MNE∥平面PBC,取CD中点E,连接ME,NE,根据中位线可知ME∥PC,NE∥BC,又ME,NE?平面MNE,ME∩NE=E,满足平面与平面平行的判定定理,最后根据性质定理可知结论;
(2)利用面积射影法,求出二面角C-BP-D的大小.
解答 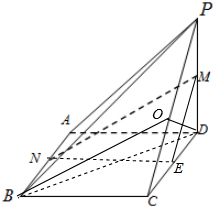 (1)证明:取CD中点E,连接ME,NE,
(1)证明:取CD中点E,连接ME,NE,
由已知M、N分别是PD、AB的中点,
∴ME∥PC,NE∥BC
又ME,NE?平面MNE,ME∩NE=E,
所以,平面MNE∥平面PBC,
所以,MN∥平面PBC;
(2)解:作DO⊥PC,则DO⊥平面PBC,△OPB为△DPB在平面中的射影,
因为△OPB中,PO=$\sqrt{2}$,所以S△OPB=$\frac{1}{2}×\sqrt{2}×2$=$\sqrt{2}$.
因为△DPB中,PD=2,BD=2$\sqrt{2}$,所以S△DPB=$\frac{1}{2}×2\sqrt{2}×2$=2$\sqrt{2}$,
所以二面角C-BP-D的余弦值为$\frac{1}{2}$,大小为60°.
点评 本小题主要考查直线与平面的位置关系、二面角及其平面角等有关知识,考查空间想象能力和思维能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.方程|x2-4x+3|=a有且仅有三个不等实数根,则实数a满足( )
| A. | a=1 | B. | a>1或a=0 | C. | 0<a≤1 | D. | 0<a<1 |
9.下列关于命题的说法正确的是( )
| A. | 命题“若x2=1则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 命题“幂函数f(x)=(m2-m-1)xm在(0,+∞)上为增函数,则m=-1”为真命题 | |
| C. | 命题“若x=y则sinx=siny”的逆否命题为真命题 | |
| D. | 命题“?x0∈R,x02+x0+1<0”的否定是“?x∈R,x2+x+1>0” |
6.两直线3x-2y-1=0与3x-2y+1=0平行,则它们之间的距离为( )
| A. | 4 | B. | $\frac{2}{13}\sqrt{13}$ | C. | $\frac{5}{26}\sqrt{13}$ | D. | $\frac{7}{20}\sqrt{10}$ |