题目内容
已知直线l1:(a-1)x+y+b=0,l2:ax+by-4=0,求满足下列条件的a,b的值
(1)l1⊥l2,且l1过(1,1)点;
(2)l1∥l2,且l2在第一象限内与两坐标轴围成的三角形的面积为2.
(1)l1⊥l2,且l1过(1,1)点;
(2)l1∥l2,且l2在第一象限内与两坐标轴围成的三角形的面积为2.
考点:直线的一般式方程与直线的垂直关系,直线的一般式方程与直线的平行关系
专题:直线与圆
分析:(1)由题意可得a(a-1)+b=0,a+b=0,联立方程组,解方程组验证可得;
(2)由平行可得a-b(a-1)=0,由面积和截距可得
×
×
=2,联立解方程组可得.
(2)由平行可得a-b(a-1)=0,由面积和截距可得
| 1 |
| 2 |
| 4 |
| a |
| 4 |
| b |
解答:
解:(1)∵l1⊥l2,∴a(a-1)+b=0,①
又l1过(1,1)点,∴a+b=0,②
联立①②可解得
或
,
当a=b=0时不合题意,应舍去,
∴a=2,b=-2;
(2)∵l1∥l2,∴a-b(a-1)=0,①
直线l2与坐标轴的交点分别为(
,0),(0,
),
由题意可得a>0且b>0,
×
×
=2,可得ab=4,②,
由①②解得a=2,b=2
又l1过(1,1)点,∴a+b=0,②
联立①②可解得
|
|
当a=b=0时不合题意,应舍去,
∴a=2,b=-2;
(2)∵l1∥l2,∴a-b(a-1)=0,①
直线l2与坐标轴的交点分别为(
| 4 |
| a |
| 4 |
| b |
由题意可得a>0且b>0,
| 1 |
| 2 |
| 4 |
| a |
| 4 |
| b |
由①②解得a=2,b=2
点评:本题考查直线的一般式方程和垂直关系,涉及三角形的面积公式和截距,属基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
已知直线l过点(-1,0),当直线l与圆x2+y2=2x有两个交点时,其斜率k的取值范围是( )
A、(-
| ||||||||
B、(-
| ||||||||
| C、(-1,1) | ||||||||
D、(-
|
已知函数f(x)=
,若f(m)>f(-m),则实数m的取值范围是( )
|
| A、(-1,0)∪(0,1) |
| B、(-∞,-1)∪(1,+∞) |
| C、(-1,0)∪(1,+∞) |
| D、(-∞,-1)∪(0,1) |
已知命题p:3<2,命题q:3>2,则下列判断正确的是( )
| A、“¬p”为真命题 |
| B、“¬q”为真命题 |
| C、“p∨q”为假命题 |
| D、“p∧q”为真命题 |
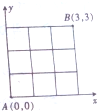 如图,电子青蛙从点A(0,0)出发,每跳一步只向上或右跳一单位长度,设每跳一步相互独立,且向上或向右的概率都为
如图,电子青蛙从点A(0,0)出发,每跳一步只向上或右跳一单位长度,设每跳一步相互独立,且向上或向右的概率都为