已知正实数x.y满足xy=1.若81x2+y2≥m恒成立.则实数m的取值范围为( )A．(-∞.9]B．(-∞.18]C．[9.+∞)D．[18.+∞) 题目和参考答案——青夏教育精英家教网—

题目内容

11．已知正实数x，y满足xy=1，若81x²+y²≥m恒成立，则实数m的取值范围为（　　）

A．

（-∞，9]

B．

（-∞，18]

C．

[9，+∞）

D．

[18，+∞）

分析 81x²+y²≥2$\sqrt{81{x}^{2}{y}^{2}}=18$，m≤（81x²+y^2）_min 即可．

解答解：81x²+y²≥2$\sqrt{81{x}^{2}{y}^{2}}=18$，由81x²+y²≥m恒成立⇒m≤（81x²+y^2）_min，∴m≤18．
故选：B

点评题考查基本不等式等知识，恒成立问题转化为函数最值问题是解决恒成立问题的常用方法，属于基础题．

练习册系列答案

相关题目

1．

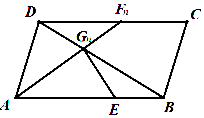如图，已知点E为平行四边形ABCD的边AB上一点，$\overrightarrow{AE}$=2$\overrightarrow{EB}$，F_n（n∈N^*）为边DC上的一列点，连接AF_n交BD于G_n，点G_n（n∈N^*）满足$\overrightarrow{{G_n}D}$=$\frac{1}{3}$a_n+1$\overrightarrow{{G_n}A}$-（3a_n+2）$\overrightarrow{{G_n}E}$，其中数列{a_n}是首项为1的正项数列，则a₄的值为（　　）

2．（1）在等差数列{a_n}中，S₁₀=50，S₂₀=300，求通项a_n．
（2）已知正数等比数列{a_n}的前n项和S_n，且S₃=a₂+10a₁，a₅=81，求S_n．

19．已知命题p：实数x满足-2$≤1-\frac{x-1}{3}$≤2，命题q：实数x满足[x-（1+m）][x-（1-m）]≤0（m＞0），若￢p是￢q的必要不充分条件，求实数m的取值范围．

6．

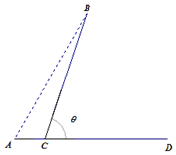某城市A计划每天从蔬菜基地B处给本市供应蔬菜，为此，准备从主干道AD的C处（不在端点A、D处）做一条道路CB，主干道AD的长为60千米，设计路线如图所示，测得蔬菜基地B在城市A的东偏北60^°处，AB长为60千米，设∠BCD=θ，运输汽车在主干道AD上的平均车速为60千米/小时，在道路CB上的平均车速为20千米/小时．
（1）求运输汽车从城市A到蔬菜基地B处所用的时间t关于θ的函数关系式t（θ），并指出其定义域；
（2）求运输汽车从城市A到蔬菜基地B处所用的时间t的最小值．

16．

甲、乙两名同学在五次考试中的数学成绩统计用茎叶图表示如图所示，则甲、乙两名同学成绩稳定的是乙．

3．将函数f（x）=Asin（ωx+ϕ）（ω＞0，|ϕ|＜$\frac{π}{2}$）的图象向右平移$\frac{π}{12}$单位后得到的函数图象关于直线x=$\frac{π}{2}$对称，且平移后所得函数的单调递增区间为$（0，\frac{π}{2}）$，则实数ϕ的值为$-\frac{π}{3}$．

20．

如图所示，五面体ABCDFE中，AB∥CD∥EF，四边形ABCD，ABEF，CDFE都是等腰梯形，并且平面ABCD⊥平面ABEF，AB=12，CD=3，EF=4，梯形ABCD的高为3，EF到平面ABCD的距离为6，则此五面体的体积为57．

1．设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{\sqrt{3}}{2}$，已知点P（0，$\frac{3}{2}$）到椭圆上的点的最远距离是$\frac{7}{4}$，则短半轴之长b=（　　）

试题分类