题目内容
已知关于x的方程x2+（4+i）x+3+pi=0（p∈R）有实数根，求p的值，并解这个方程．
考点：复数代数形式的混合运算
专题：数系的扩充和复数
分析：设方程的实数根为a，利用复数相等的等价条件进行求解即可．
解答：
解：设方程的实数根为a，
则满足a2+（4+i）a+3+pi=0，
即a2+4a+3+（a+p）i=0，
则
，
即
，
则当a=-1时，p=1；当a=-3时，p=3，
当a=-1，p=1时，由韦达定理得-1+x=-（4+i），即x=-3+i，即另外一个根为-3+i，
当a=-3，p=3时，由韦达定理得-3+x=-（4+i），即x=-1+i，即另外一个根为-1+i．
则满足a2+（4+i）a+3+pi=0，
即a2+4a+3+（a+p）i=0，
则
|
即
|
则当a=-1时，p=1；当a=-3时，p=3，
当a=-1，p=1时，由韦达定理得-1+x=-（4+i），即x=-3+i，即另外一个根为-3+i，
当a=-3，p=3时，由韦达定理得-3+x=-（4+i），即x=-1+i，即另外一个根为-1+i．
点评：本题主要考查复数方程的求解，利用复数相等是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知A、B、C为三个不共线的点，P为△ABC所在平面内一点，若
+
=
+
，则点P与△ABC的位置关系是（ ）
| PA |
| PB |
| PC |
| AB |
| A、点P在△ABC内部 |
| B、点P在△ABC外部 |
| C、点P在直线AB上 |
| D、点P在直线AC上 |
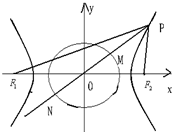如图F1，F2为双曲线C：
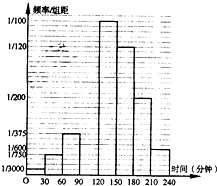为了调查学生星期天晚上学习时间利用问题，某校从高二年级1000名学生（其中走读生450名，住宿生500名）中，采用分层抽样的方法抽取n名学生进行问卷调查．根据问卷取得了这n名同学每天晚上学习时间（单位：分钟）的数据，按照以下区间分为八组①[0，30），②[30，60），③[60，90），④[90，120），⑤[120，150），⑥[150，180），⑦[180，210），⑧[210，240]，得到频率分布直方图如图所示．已知抽取的学生中星期天晚上学习时间少于60分钟的人数为5人；