题目内容
设集合M={x|x2≤4},N={-1,0,4},则M∩N=( )
| A、{-1,0,4} |
| B、{-1,0} |
| C、{0,4} |
| D、{-2,-1,0} |
考点:交集及其运算
专题:集合
分析:先求出不等式x2≤4的解集M,再由交集的运算求出M∩N.
解答:
解:由x2≤4得-2≤x≤2,
则集合M={x|-2≤x≤2},
又N={-1,0,4},
所以M∩N={-1,0},
故选:B.
则集合M={x|-2≤x≤2},
又N={-1,0,4},
所以M∩N={-1,0},
故选:B.
点评:本题考查交集及其运算,以及一元二次不等式的解法,属于基础题.

练习册系列答案
相关题目
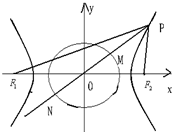 如图F1,F2为双曲线C:
如图F1,F2为双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
| A、5 | B、30 | C、225 | D、15 |
设等差数列{an}的前n项和为Sn,且S3=6,a1=4,则公差d等于( )
| A、-2 | ||
| B、1 | ||
C、
| ||
| D、3 |
如图是一个算法的流程图,若输出的结果是255,则判断框中的整数N的值为( )


| A、6 | B、7 | C、8 | D、9 |