题目内容
某工厂现有200人,人均年收入为4万元.为了提高工人的收入,工厂将进行技术改造,改造后有x(100≤x≤150)人继续留用,他们的人均年收入为4a(a∈N+)万元,剩下的人从事其它服务行业,这些人的人均年收入有望提高(2x)%.
(1)设技术改造后这200人的人均年收入为y万元,求出y与x之间的函数关系式;
(2)当x为多少时,能使这200人的人均年收入达到最大,并求出最大值.
(1)设技术改造后这200人的人均年收入为y万元,求出y与x之间的函数关系式;
(2)当x为多少时,能使这200人的人均年收入达到最大,并求出最大值.
考点:函数模型的选择与应用
专题:函数的性质及应用
分析:(1)根据条件建立函数关系即可求出y与x之间的函数关系式;
(2)结合函数关系以及一元二次函数的单调性,即可求出函数的最值.
(2)结合函数关系以及一元二次函数的单调性,即可求出函数的最值.
解答:
解:(1)由题意可知技术改造后这200人的人均年收入为y=
=-
x2+
•x+1,(100≤x≤150).
(2)因为函数y=f(x)=-
x2+
•x+1为开口向下的抛物线,
所以对称轴x=-
=
=100a+75,
因为a∈N+),所以对称轴x=100a+75≥175,
所以当100≤x≤150是,函数y=f(x)单调递增,
故当x=150时,函数取得最大值为f(150)=3a+1(万元).
答当x150时,能使这200人的人均年收入达到最大,最大值为3a+1(万元).
4ax+(200-x)(1+
| ||
| 200 |
| 1 |
| 10000 |
| 4a+3 |
| 200 |
(2)因为函数y=f(x)=-
| 1 |
| 10000 |
| 4a+3 |
| 200 |
所以对称轴x=-
| ||
2×(-
|
| 50(5a+3) |
| 2 |
因为a∈N+),所以对称轴x=100a+75≥175,
所以当100≤x≤150是,函数y=f(x)单调递增,
故当x=150时,函数取得最大值为f(150)=3a+1(万元).
答当x150时,能使这200人的人均年收入达到最大,最大值为3a+1(万元).
点评:本题主要考查函数的应用问题,根据条件建立函数关系,利用一元二次函数的性质是解决本题的关键.

练习册系列答案
相关题目
直线ax-y+2a=0与曲线y=
相交于相异两点,则实数a的取值范围是( )
| 4-(x-1)2 |
A、[-
| ||||||||
B、(-
| ||||||||
C、[0,
| ||||||||
D、[0,
|
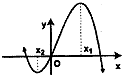 已知函数f(x)=ax3+bx2+x(a,b∈R,ab≠0)的图象如图所示(x1,x2为两个极值点),且|x1|>|x2|则有( )
已知函数f(x)=ax3+bx2+x(a,b∈R,ab≠0)的图象如图所示(x1,x2为两个极值点),且|x1|>|x2|则有( )| A、a>0,b>0 |
| B、a<0,b<0 |
| C、a<0,b>0 |
| D、a>0,b<0 |