题目内容
已知方程
+
=1（m∈R）表示双曲线的实数m的取值集合A，设不等式x2-（a2-3）x-3a2＜0的解集为B，若x∈A是x∈B的充分不必要条件，则实数a的取值范围是 ．
| x2 |
| m |
| y2 |
| m-4 |
考点：必要条件、充分条件与充要条件的判断
专题：不等式的解法及应用,圆锥曲线的定义、性质与方程,简易逻辑
分析：先分别根据双曲线的定义求出集合A，再解二次不等式求出集合B，再将条件“m∈A是m∈B的充分不必要条件”转化为A⊆B，从而可求参数a的范围．
解答：
解：若方程
+
=1（m∈R）表示双曲线，
则m（m-4）＜0，解得：0＜m＜4，
故A=（0，4），
解x2-（a2-3）x-3a2=0得：x=-3，或x=a2，
故B=（-3，a2），
∵x∈A是x∈B的充分不必要条件，
∴A⊆B，
∴a2≥4，
解得：a∈（-∞，-2]∪[2，+∞），
故实数a的取值范围是（-∞，-2]∪[2，+∞），
故答案为：（-∞，-2]∪[2，+∞）
| x2 |
| m |
| y2 |
| m-4 |
则m（m-4）＜0，解得：0＜m＜4，
故A=（0，4），
解x2-（a2-3）x-3a2=0得：x=-3，或x=a2，
故B=（-3，a2），
∵x∈A是x∈B的充分不必要条件，
∴A⊆B，
∴a2≥4，
解得：a∈（-∞，-2]∪[2，+∞），
故实数a的取值范围是（-∞，-2]∪[2，+∞），
故答案为：（-∞，-2]∪[2，+∞）
点评：本题考查必要条件、充分条件、充要条件的判断，解题时要认真审题，仔细解答，属于基础题．
练习册系列答案
一本好题口算题卡系列答案
相关题目
设集合A={x|x+2＞0}，B={x|y=
}，则A∩B=（ ）
| 1 | ||
|
| A、{x|x＞-2} |
| B、{x|x＜3} |
| C、{x|x＞3或x＜-2} |
| D、{x|-2＜x＜3} |
如图，在正方体ABCD-A1B1C1D1中，B1E1=D1F1=直线ax-y+2a=0与曲线y=
相交于相异两点，则实数a的取值范围是（ ）
| 4-(x-1)2 |
A、[-
| ||||||||
B、（-
| ||||||||
C、[0，
| ||||||||
D、[0，
|
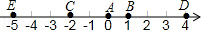如图，A点的初始位置位于数轴上的原点，现对A点做如下移动：第1次从原点向右移动1个单位长度至B点，第2次从B点向左移动3个单位长度至C点，第3次从C点向右移动6个单位长度至D点，第4次从D点向左移动9个单位长度至E点，…，依此类推，这样移动解答：