题目内容
在数列{an}中,已知a2=1,前n项和为Sn,且Sn=
.(其中n∈N*)
(1)求a1;
(2)求数列{an}的通项公式;
(3)设lgbn=
,问是否存在正整数p、q(其中1<p<q),使得b1,bp,bq成等比数列?若存在,求出所有满足条件的数组(p,q);否则,说明理由.
| n(an-a1) |
| 2 |
(1)求a1;
(2)求数列{an}的通项公式;
(3)设lgbn=
| an+1 |
| 3n |
考点:数列递推式,数列的求和
专题:函数的性质及应用,等差数列与等比数列
分析:(1)直接利用n=1求出数列的首项.
(2)利用递推关系式和叠乘法求数列的通项公式.
(3)存在性问题的判断,先假设存在,然后利用函数的单调性判断存在有序实数对.
(2)利用递推关系式和叠乘法求数列的通项公式.
(3)存在性问题的判断,先假设存在,然后利用函数的单调性判断存在有序实数对.
解答:
解:(1)因为Sn=
,
令n=1,得a1=
=0,
所以a1=0;
或者令n=2,得a1+a2=
,
所以:a1=0
(2)当n≥2时,Sn+1=
=
,an+1=Sn+1-Sn=
-
,
=
,
推得
=
,
利用叠乘法求出数列an=n-1
又a2=1,a3=2a2=3,
所以an+1=n,
当n=1,2时也成立,
所以an=n-1,(n∈N*)
(3)假设存在正整数p,q使得b1,bp,bq成等比数列,
则:lgb1,lgbp,lgbq成等差数列.
则:
=
+
①
由于等式右边大于
,
故
>
则:
>
下面考察数列{
}d的单调性.
因为:
-
=
<0
故数列{
}是单调递减数列.
当p=2时,
=
>
代入①式得::
=
解得:q=3
当p≥3时,
≤
(舍去)
故存在(p,q)为(2,3)使得b1,bp,bq成等比数列.
| n(an-a1) |
| 2 |
令n=1,得a1=
| (a1-a1) |
| 2 |
所以a1=0;
或者令n=2,得a1+a2=
| 2(a2-a1) |
| 2 |
所以:a1=0
(2)当n≥2时,Sn+1=
| (n+1)(an+1-a1) |
| 2 |
| (n+1)an+1 |
| 2 |
| (n+1)an+1 |
| 2 |
| nan |
| 2 |
| an+1 |
| an |
| n |
| n-1 |
推得
| an+1 |
| a3 |
| n |
| 3-1 |
利用叠乘法求出数列an=n-1
又a2=1,a3=2a2=3,
所以an+1=n,
当n=1,2时也成立,
所以an=n-1,(n∈N*)
(3)假设存在正整数p,q使得b1,bp,bq成等比数列,
则:lgb1,lgbp,lgbq成等差数列.
则:
| 2p |
| 3p |
| q |
| 3q |
| 1 |
| 3 |
由于等式右边大于
| 1 |
| 3 |
故
| 2p |
| 3p |
| 1 |
| 3 |
则:
| p |
| 3p |
| 1 |
| 6 |
下面考察数列{
| p |
| 3p |
因为:
| p+1 |
| 3p+1 |
| p |
| 3p |
| 1-2p |
| 3p+1 |
故数列{
| p |
| 3p |
当p=2时,
| p |
| 3p |
| 2 |
| 9 |
| 1 |
| 6 |
| q |
| 3q |
| 1 |
| 9 |
解得:q=3
当p≥3时,
| p |
| 3p |
| 1 |
| 9 |
故存在(p,q)为(2,3)使得b1,bp,bq成等比数列.
点评:本题考查的知识要点:利用递推关系式和叠乘法求数列的通项公式,利用函数的单调性判断存在性问题.属于中等题型.

练习册系列答案
相关题目
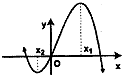 已知函数f(x)=ax3+bx2+x(a,b∈R,ab≠0)的图象如图所示(x1,x2为两个极值点),且|x1|>|x2|则有( )
已知函数f(x)=ax3+bx2+x(a,b∈R,ab≠0)的图象如图所示(x1,x2为两个极值点),且|x1|>|x2|则有( )| A、a>0,b>0 |
| B、a<0,b<0 |
| C、a<0,b>0 |
| D、a>0,b<0 |
 如图,焦点在x轴的椭圆C:
如图,焦点在x轴的椭圆C: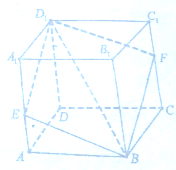 如图,在棱长为1的正方体ABCD-A1B1C1D1中,过对角线BD1的平面分别交AA1,CC1于点E,F.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,过对角线BD1的平面分别交AA1,CC1于点E,F.