题目内容
7. 已知$\overrightarrow{a}$=2(cosωx,cosωx),$\overrightarrow{b}$=(cosωx,$\sqrt{3}$sinωx)(其中0<ω<1),函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$,
已知$\overrightarrow{a}$=2(cosωx,cosωx),$\overrightarrow{b}$=(cosωx,$\sqrt{3}$sinωx)(其中0<ω<1),函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$,(1)若直线x=$\frac{π}{3}$是函数f(x)图象的一条对称轴,先列表再作出函数f(x)在区间[-π,π]上的图象.
(2)求函数y=f(x),x∈[-π,π]的值域.
分析 (1)利用两个向量的数量积公式,三角恒等变换化简函数的解析式,再用用五点法作函数y=f(x)在区间[-π,π]上的图象.
(2)由题意利用正弦函数的定义域和值域,求得函数y=f(x),x∈[-π,π]的值域.
解答 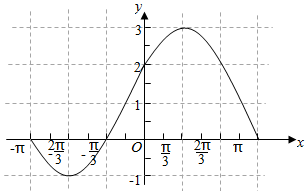 解:(1)函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$=2cos2ωx+2$\sqrt{3}$sinωxcosωx=cos2ωx+$\sqrt{3}$sin2ωx+1=2sin(2ωx+$\frac{π}{6}$)+1,
解:(1)函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$=2cos2ωx+2$\sqrt{3}$sinωxcosωx=cos2ωx+$\sqrt{3}$sin2ωx+1=2sin(2ωx+$\frac{π}{6}$)+1,
若直线x=$\frac{π}{3}$是函数f(x)图象的一条对称轴,则2ω•$\frac{π}{3}$+$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,
即ω=$\frac{3k}{2}$+$\frac{1}{2}$,k∈Z,
结合0<ω<1,可得ω=$\frac{1}{2}$,故f(x)=2sin(x+$\frac{π}{6}$)+1.
列表:
| x+$\frac{π}{6}$ | -$\frac{5π}{6}$ | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | π | $\frac{7π}{6}$ |
| x | -π | -$\frac{2π}{3}$ | -$\frac{π}{6}$ | $\frac{π}{3}$ | $\frac{5π}{6}$ | π |
| y | 0 | -1 | 1 | 3 | 1 | 0 |
(2)根据x∈[-π,π],可得x+$\frac{π}{6}$∈[-$\frac{5π}{6}$,$\frac{7π}{6}$],sin(x+$\frac{π}{6}$)∈[-1,1],故函数f(x)的值域为[-1,3].
点评 本题主要考查两个向量的数量积公式,三角恒等变换,用五点法作函数y=Asin(ωx+φ)的图象,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
17.△ABC的三个内角为A、B、C,若$\frac{{sinA+\sqrt{3}cosA}}{{cosA-\sqrt{3}sinA}}=tan\frac{7π}{12}$,则sin2B+2cosC的最大值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
15.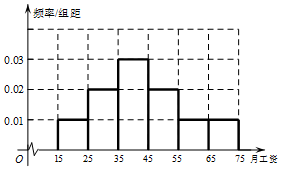 为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
(1)试由图估计该单位员工月平均工资;
(2)现用分层抽样的方法从月工资在[45,55)和[55,65)的两组所调查的男员工中随机选取5人,问各应抽取多少人?
(3)若从月工资在[25,35)和[45,55)两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
 为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:| 月工资 (单位:百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
| 女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |
(2)现用分层抽样的方法从月工资在[45,55)和[55,65)的两组所调查的男员工中随机选取5人,问各应抽取多少人?
(3)若从月工资在[25,35)和[45,55)两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
12.已知{an}是等比数列,那么下列结论错误的是( )
| A. | ${a_5}^2={a_3}•{a_7}$ | B. | ${a_5}^2={a_1}•{a_9}$ | ||
| C. | ${a_n}^2={a_{n-1}}•{a_{n+1}}({n∈{N^*}})$ | D. | ${a_n}^2={a_{n-k}}•{a_{n+k}}({k∈{N^*},n>k>0})$ |
19.国内某汽车品牌一个月内被消费者投诉的次数用X表示,据统计,随机变量X的概率分布如下:
(1)求a的值;
(2)假设一月份与二月份被消费者投诉的次数互不影响,求该汽车品牌在这两个月内共被消费者投诉2次的概率.
| X | 0 | 1 | 2 | 3 |
| P | 0.1 | 0.3 | 2a | a |
(2)假设一月份与二月份被消费者投诉的次数互不影响,求该汽车品牌在这两个月内共被消费者投诉2次的概率.