题目内容
5.已知函数f(x)=ax2-2ax+b,当x∈[0,3]时,|f(x)|≤1恒成立,则2a+b的最大值为1.分析 通过讨论a的符号,得到f(x)的最小值和最大值,由恒成立思想可得a,b满足的条件,作出可行域,从而求出2a+b的最大值即可.
解答  解:f(x)=ax2-2ax+b=a(x-1)2+b-a,
解:f(x)=ax2-2ax+b=a(x-1)2+b-a,
则函数的对称轴为x=1,最值为b-a,
当a>0时,函数f(x)图象开口向上,
当x=1时,f(x)取最小值b-a,
当x=3时取最大值3a+b,
由|f(x)|≤1恒成立,即-1≤f(x)≤1在[0,3]恒成立,
可得-1≤b-a,且3a+b≤1,且a>0,
作出点(a,b)满足的不等式组的可行域,如上图.
则z=2a+b过点(0,1)时,取得最大值1;
当a<0时,函数f(x)图象开口向下,
当x=1时,f(x)取最大值b-a,
当x=3时取最小值3a+b,
由|f(x)|≤1恒成立,即-1≤f(x)≤1在[0,3]恒成立,
可得-1≤3a+b,且-a+b≤1,且a<0,
作出点(a,b)满足的不等式组的可行域,如下图.
则z=2a+b过点(0,1)时,取得最大值1.
故答案为:1.
点评 本题考查了二次函数的性质,考查分类讨论思想,注意运用线性规划求最值,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.△ABC的三个内角为A、B、C,若$\frac{{sinA+\sqrt{3}cosA}}{{cosA-\sqrt{3}sinA}}=tan\frac{7π}{12}$,则sin2B+2cosC的最大值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
15.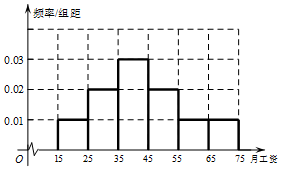 为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
(1)试由图估计该单位员工月平均工资;
(2)现用分层抽样的方法从月工资在[45,55)和[55,65)的两组所调查的男员工中随机选取5人,问各应抽取多少人?
(3)若从月工资在[25,35)和[45,55)两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
 为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:| 月工资 (单位:百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
| 女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |
(2)现用分层抽样的方法从月工资在[45,55)和[55,65)的两组所调查的男员工中随机选取5人,问各应抽取多少人?
(3)若从月工资在[25,35)和[45,55)两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
 在四棱锥P-ABCD中,已知DC∥AB,DC=2AB,E为棱PD的中点.
在四棱锥P-ABCD中,已知DC∥AB,DC=2AB,E为棱PD的中点.