题目内容
10.设数列{an}的前n项和为Sn,若对于任意的n∈N*,都有Sn=2an-3n.(1)求证{an+3}是等比数列
(2)求数列{an}的通项公式;
(3)求数列{an}的前n项和Sn.
分析 (1)令n=1,则a1=S1=2a1-3.求出a1=3,由Sn+1=2an+1-3(n+1),得Sn=2an-3n,两式相减,推导出an+1+3=2(an+3),由此能证明{an+3}是首项为6,公比为2的等比数列.
(2)由an+3=6×2n-1,能求出数列{an}的通项公式.
(3)由an=6×2n-1-3,能求出数列{an}的前n项和.
解答 证明:(1)∵数列{an}的前n项和为Sn,对于任意的n∈N*,都有Sn=2an-3n.
∴令n=1,则a1=S1=2a1-3.解得a1=3,
又Sn+1=2an+1-3(n+1),Sn=2an-3n,
两式相减得,
an+1=2an+1-2an-3,则an+1=2an+3,
∴an+1+3=2(an+3),
又a1+3=6,
∴{an+3}是首项为6,公比为2的等比数列.
解:(2)∵{an+3}是首项为6,公比为2的等比数列.
∴an+3=6×2n-1,∴an=6×2n-1-3.
(3)∵an=6×2n-1-3.
∴数列{an}的前n项和:
Sn=6×$\frac{1-{2}^{n}}{1-2}$-3n=6×2n-3n-6.
点评 本题考查等比数列的证明,考查数列的通项公式及前n项和的求法,考查等比数列、构造法等基础知识,考查运算求解能力、数据处理能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
1.若直线x+2y+a=0过圆x2+y2+2x-4y+1=0的圆心,则实数a的值为( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
15.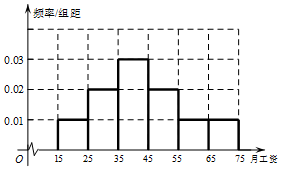 为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
(1)试由图估计该单位员工月平均工资;
(2)现用分层抽样的方法从月工资在[45,55)和[55,65)的两组所调查的男员工中随机选取5人,问各应抽取多少人?
(3)若从月工资在[25,35)和[45,55)两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
 为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:| 月工资 (单位:百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
| 女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |
(2)现用分层抽样的方法从月工资在[45,55)和[55,65)的两组所调查的男员工中随机选取5人,问各应抽取多少人?
(3)若从月工资在[25,35)和[45,55)两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
19.国内某汽车品牌一个月内被消费者投诉的次数用X表示,据统计,随机变量X的概率分布如下:
(1)求a的值;
(2)假设一月份与二月份被消费者投诉的次数互不影响,求该汽车品牌在这两个月内共被消费者投诉2次的概率.
| X | 0 | 1 | 2 | 3 |
| P | 0.1 | 0.3 | 2a | a |
(2)假设一月份与二月份被消费者投诉的次数互不影响,求该汽车品牌在这两个月内共被消费者投诉2次的概率.