题目内容
设函数f(x)=
.
(1)求函数f(x)在[
,2]上的最值;
(2)证明:对任意正数a,存在正数x,使不等式f(x)-1<a成立.
| ex-1 |
| x |
(1)求函数f(x)在[
| 1 |
| 2 |
(2)证明:对任意正数a,存在正数x,使不等式f(x)-1<a成立.
考点:利用导数求闭区间上函数的最值,导数在最大值、最小值问题中的应用
专题:计算题,导数的综合应用
分析:(1)f′(x)=
,令h(x)=(x-1)ex+1,则h′(x)=x•ex,从而由导数的正负确定函数的单调性,从而求最值;
(2)化简不等式f(x)-1<a为ex-(a+1)x-1<0,求导讨论函数的单调性,从而求函数的最小值,证明最小值小于0即可.
| (x-1)ex+1 |
| x2 |
(2)化简不等式f(x)-1<a为ex-(a+1)x-1<0,求导讨论函数的单调性,从而求函数的最小值,证明最小值小于0即可.
解答:
解:(1)f′(x)=
,
令h(x)=(x-1)ex+1,则h′(x)=x•ex,
故h(x)=(x-1)ex+1在(0,+∞)上是增函数,
又∵h(0)=0,
故f(x)=
在(0,+∞)上是增函数,
则函数f(x)在[
,2]上的最小值为f(
)=2
-2,
最大值为f(2)=
e2-
;
(2)证明:f(x)-1=
,
不等式f(x)-1<a可化为ex-(a+1)x-1<0,
令g(x)=ex-(a+1)x-1,则g′(x)=ex-(a+1),
令ex-(a+1)=0解得,x=ln(a+1),
故当0<x<ln(a+1)时,g′(x)<0,
当x>ln(a+1)时,g′(x)>0,
则当x=ln(a+1)时,gmin(x)=a-(a+1)ln(a+1),
令m(a)=
-ln(a+1),(a≥0),
则m′(a)=-
<0,
则当a>0时,m(a)<m(0)=0;
故gmin(x)=a-(a+1)ln(a+1)<0,
故存在正数x,使不等式f(x)-1<a成立.
| (x-1)ex+1 |
| x2 |
令h(x)=(x-1)ex+1,则h′(x)=x•ex,
故h(x)=(x-1)ex+1在(0,+∞)上是增函数,
又∵h(0)=0,
故f(x)=
| ex-1 |
| x |
则函数f(x)在[
| 1 |
| 2 |
| 1 |
| 2 |
| e |
最大值为f(2)=
| 1 |
| 2 |
| 1 |
| 2 |
(2)证明:f(x)-1=
| ex-x-1 |
| x |
不等式f(x)-1<a可化为ex-(a+1)x-1<0,
令g(x)=ex-(a+1)x-1,则g′(x)=ex-(a+1),
令ex-(a+1)=0解得,x=ln(a+1),
故当0<x<ln(a+1)时,g′(x)<0,
当x>ln(a+1)时,g′(x)>0,
则当x=ln(a+1)时,gmin(x)=a-(a+1)ln(a+1),
令m(a)=
| a |
| a+1 |
则m′(a)=-
| a |
| (a+1)2 |
则当a>0时,m(a)<m(0)=0;
故gmin(x)=a-(a+1)ln(a+1)<0,
故存在正数x,使不等式f(x)-1<a成立.
点评:本题考查了导数的综合应用,属于中档题.

练习册系列答案
相关题目
若M={x|x>1},N={x|x≥a},且N⊆M,则( )
| A、a≤1 | B、a≥1 |
| C、a<1 | D、a>1 |
已知抛物线y2=2px(p>0)上一点M(1,m)(m>0)到其焦点F的距离为5,该抛物线的顶点在直线MF上的射影为点P,则点P的坐标为( )
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
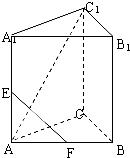 如图,在正三棱柱ABC-A1B1C1中,AC=2,AC1与底面成60°角,E、F分别为AA1、AB的中点.
如图,在正三棱柱ABC-A1B1C1中,AC=2,AC1与底面成60°角,E、F分别为AA1、AB的中点. 如图1,在Rt△ACB中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
如图1,在Rt△ACB中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.