题目内容
函数f（x）=
的图象在点（1，-2）处的切线方程为（ ）
| lnx-2x |
| x |
| A、2x-y-4=0 |
| B、2x+y=0 |
| C、x-y-3=0 |
| D、x+y+1=0 |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：求出曲线的导函数，把x=1代入即可得到切线的斜率，然后根据（1，2）和斜率写出切线的方程即可．
解答：
解：由函数f（x）=
知f′（x）=
，
把x=1代入得到切线的斜率k=1，
则切线方程为：y+2=x-1，
即x-y-3=0．
故选：C．
| lnx-2x |
| x |
| 1-lnx |
| x2 |
把x=1代入得到切线的斜率k=1，
则切线方程为：y+2=x-1，
即x-y-3=0．
故选：C．
点评：本题考查学生会利用导数求曲线上过某点的切线方程，考查计算能力，注意正确求导．
练习册系列答案
相关题目
已知函数f（x）=
，则f（2014）的值为（ ）
|
A、
| ||
| B、2 | ||
C、-
| ||
| D、-2 |
设函数f（x）=（x-1）kcosx（k∈N*），则（ ）
| A、当k=2013时，f（x）在x=1处取得极小值 |
| B、当k=2013时，f（x）在x=1处取得极大值 |
| C、当k=2014时，f（x）在x=1处取得极小值 |
| D、当k=2014时，f（x）在x=1处取得极大值 |
已知i是虚数单位，若（m+i）2=3-4i，则实数m的值为（ ）
| A、-2 | ||
| B、±2 | ||
C、±
| ||
| D、2 |
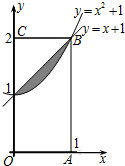如图，在矩形OABC内：记抛物线y=x2+1与直线y=x+1围成的区域为M（图中阴影部分）．随机往矩形OABC内投一点P，则点P落在区域M内的概率是（ ）