题目内容
正方体ABCD-A1B1C1D1中,M,N,P,Q分别是棱B1C1,C1D1,D1A1,BC的中点,则异面直线MN与PQ所成的角等于 .
考点:异面直线及其所成的角
专题:空间位置关系与距离
分析:建立空间直角坐标系利用向量方法求直线EF与MN的夹角;
解答:
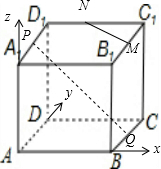 解:以A为坐标原点,建立空间直角坐标系如图:
解:以A为坐标原点,建立空间直角坐标系如图:
设正方体的棱长为1,
则A(0,0,0),B(1,0,0),P(0,
,1),Q(1,
,0),
M(1,
,1),N(
,1,1),
则
=(1,0,-1),
=(-
,
,0),
设异面直线MN与PQ所成的角为θ,
则cosθ=
=
=
则θ=60°,
即直线PQ与MN的夹角为60°;
故答案为:60°.
 解:以A为坐标原点,建立空间直角坐标系如图:
解:以A为坐标原点,建立空间直角坐标系如图:设正方体的棱长为1,
则A(0,0,0),B(1,0,0),P(0,
| 1 |
| 2 |
| 1 |
| 2 |
M(1,
| 1 |
| 2 |
| 1 |
| 2 |
则
| PQ |
| MN |
| 1 |
| 2 |
| 1 |
| 2 |
设异面直线MN与PQ所成的角为θ,
则cosθ=
|
| ||||
|
|
| ||||||
|
| 1 |
| 2 |
则θ=60°,
即直线PQ与MN的夹角为60°;
故答案为:60°.
点评:本题主要考查二面角的求解以及利用向量法求解异面直线的角的大小,运算量较大.

练习册系列答案
相关题目
若平面向量
,
满足|2
-
|≤3,则
•
的范围是( )
| a |
| b |
| a |
| b |
| a |
| b |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、(-
|
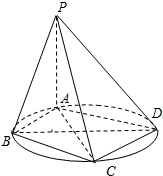 (文)如图,四棱锥P-ABCD的底面ABCD是圆内接四边形(记此圆为W),且PA⊥平面ABCD.
(文)如图,四棱锥P-ABCD的底面ABCD是圆内接四边形(记此圆为W),且PA⊥平面ABCD.