题目内容
若方程-x2+2x-m=3-x在x∈（0，3）内有唯一解，求实数m的取值范围．
考点：函数零点的判定定理
专题：函数的性质及应用
分析：若方程-x2+2x-m=3-x在x∈（0，3）内有唯一解，即方程x2-3x+m+3=0在x∈（0，3）内有唯一解，分别讨论△=0和△＞0时，满足条件的实数m的值，最后综合讨论结果可得答案．
解答：
解：若方程-x2+2x-m=3-x在x∈（0，3）内有唯一解，
即方程x2-3x+m+3=0在x∈（0，3）内有唯一解，
若△=9-4（m+3）=0，即m=-
，
此时方程有唯一解
∈（0，3）满足要求，
若△=9-4（m+3）＞0，即m＜-
，
此时方程有唯一解，即函数f（x）=x2-3x+m+3在x∈（0，3）内有唯一的零点，
即f（0）f（3）=（m+3）•（m+3）＜0，此时不存在满足条件的m值，
综上所述实数m=-
即方程x2-3x+m+3=0在x∈（0，3）内有唯一解，
若△=9-4（m+3）=0，即m=-
| 3 |
| 4 |
此时方程有唯一解
| 3 |
| 2 |
若△=9-4（m+3）＞0，即m＜-
| 3 |
| 4 |
此时方程有唯一解，即函数f（x）=x2-3x+m+3在x∈（0，3）内有唯一的零点，
即f（0）f（3）=（m+3）•（m+3）＜0，此时不存在满足条件的m值，
综上所述实数m=-
| 3 |
| 4 |
点评：本题考查的知识点是方程的根与函数的零点，其中熟练掌握函数的零点与对应方程根之间的关系是解答的关键．
练习册系列答案
名校课堂系列答案
相关题目
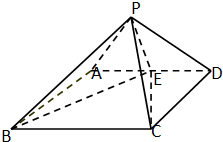如图，四棱锥P-ABCD的底面是矩形，侧面PAD⊥底面ABCD，在△PAD中