题目内容
若平面向量
,
满足|2
-
|≤3,则
•
的范围是( )
| a |
| b |
| a |
| b |
| a |
| b |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、(-
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由平面向量
,
满足|2
-
|≤3,通过平方以及基本不等式,求出
•
的最小值,即可.
| a |
| b |
| a |
| b |
| a |
| b |
解答:
解:∵平面向量
,
满足|2
-
|≤3,∴4
2+
2≤9+4
•
,
∴4
2+
2≥2
=4|
||
|≥-4
•
,
∴9+4
•
≥-4
•
,
∴
•
≥-
,
故
•
的最小值是-
.
•
的范围是:[-
,+∞).
故选:A.
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
∴4
| a |
| b |
4
|
| a |
| b |
| a |
| b |
∴9+4
| a |
| b |
| a |
| b |
∴
| a |
| b |
| 9 |
| 8 |
故
| a |
| b |
| 9 |
| 8 |
| a |
| b |
| 9 |
| 8 |
故选:A.
点评:本题考查平面向量数量积的坐标表示,是中档题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
函数y=
的单调递减区间是( )
| lnx |
| x |
| A、(e-1,+∞) |
| B、(0,e-1) |
| C、(-∞,e-1) |
| D、(e,+∞) |
当0<x<1时,f(x)=
,则下列大小关系正确的是( )
| sinx |
| x |
| A、f2(x)<f(x)<f(x2) |
| B、f(x2)<f2(x)<f(x) |
| C、f(x)<f(x2)<f2(x) |
| D、f2(x)<f(x2)<f(x) |
函数f(x)的图象如图所示,则不等式(x+3)•f′(x)<0的解集为( )
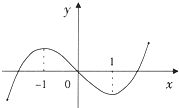

| A、(-∞,-3)∪(-1,1) |
| B、(-∞,-3) |
| C、(-∞,-1)∪(1,+∞) |
| D、(1,+∞) |
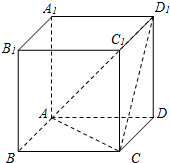 在如图所示的棱长为2的正方体ABCD-A1B1C1D1中,作与平面ACD1平行的截面,则截得的三角形中面积最大的值是
在如图所示的棱长为2的正方体ABCD-A1B1C1D1中,作与平面ACD1平行的截面,则截得的三角形中面积最大的值是