题目内容
10.已知AB是圆C:x2+y2-4x+2y+a=0的一条弦,M(1,0)是弦AB的中点,若AB=3,则实数a的值是$\frac{3}{4}$.分析 利用配方法得到圆的标准方程,求出直线方程、圆心到直线的距离,根据弦AB=3,求出圆的半径,即可得到a的值.
解答 解:圆C:x2+y2-4x+2y+a=0,即(x-2)2+(y+1)2=-a+5,
则圆心C(2,-1),半径r=$\sqrt{5-a}$,
∵弦AB的中点为M(1,0).
∴直线CM的斜率k=-1,
则直线l的斜率k=1,
则直线l的方程为y-0=x-1,即x-y-1=0.
圆心C到直线x-y-1=0的距离d=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
若弦AB=3,
则2+$\frac{9}{4}$=5-a,
解得a=$\frac{3}{4}$,
故答案为$\frac{3}{4}$.
点评 本题主要考查直线和圆的方程的应用,利用配方法将圆配成标准方程是解决本题的关键.

练习册系列答案
相关题目
20.一架战斗机以1000$\sqrt{2}$千米/小时速度朝东偏北45°方向水平飞行,发现正东100千米外同高度有一架民航飞机正在以800千米/小时速度朝正北飞行,如双方都不改变速度与航向,两机最小距离在哪个区间内(单位:千米)( )
| A. | (0,5) | B. | (5,10) | C. | (10,15) | D. | (15,20) |
2.下列各式中,最小值为2的是( )
| A. | $x+\frac{1}{x}$ | B. | $\sqrt{{x^2}+2}+\frac{4}{{\sqrt{{x^2}+2}}}$ | C. | $\frac{y}{x}+\frac{x}{y}$ | D. | $x-2\sqrt{x}+3$ |
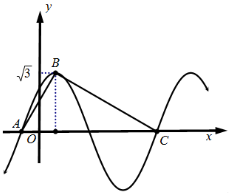 已知函数y=$\sqrt{3}$sin(ωx+$\frac{π}{4}$)(ω>0).
已知函数y=$\sqrt{3}$sin(ωx+$\frac{π}{4}$)(ω>0).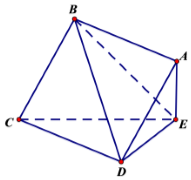 如图,边长为2的正方形ABCD所在平面与三角形CDE所在的平面相交于CD,AE⊥平面CDE,且AE=1.
如图,边长为2的正方形ABCD所在平面与三角形CDE所在的平面相交于CD,AE⊥平面CDE,且AE=1.