题目内容
18.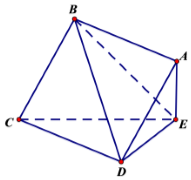 如图,边长为2的正方形ABCD所在平面与三角形CDE所在的平面相交于CD,AE⊥平面CDE,且AE=1.
如图,边长为2的正方形ABCD所在平面与三角形CDE所在的平面相交于CD,AE⊥平面CDE,且AE=1.(1)求证:AB∥平面CDE;
(2)求证:DE⊥平面ABE;
(3)求点A到平面BDE的距离.
分析 (1)推导出AB∥CD,由此能证明AB∥平面CDE.
(2)推导出AE⊥CD,DE⊥AE,从而CD⊥DE,再由DE⊥AB,能证明DE⊥平面ABE.
(3)由AB⊥平面ADE,能求出三棱锥B-ADE的体积.再由VA-BDE=VB-ADE,能求出点A到平面BDE的距离.
解答 证明:(1)∵正方形ABCD中,AB∥CD,
AB?平面CDE,CD?平面CDE,
∴AB∥平面CDE.
(2)∵AE⊥平面CDE,CD?平面CDE,DE?平面CDE,
∴AE⊥CD,DE⊥AE,
在正方形ABCD中,CD⊥AD,
∵AD∩AE=A,∴CD⊥平面ADE.
∵DE?平面ADE,∴CD⊥DE,
∵AB∥CD,∴DE⊥AB,
∵AB∩AE=E,∴DE⊥平面ABE.
解:(3)∵AB⊥AD,AB⊥DE,AD∩DE=D,
∴AB⊥平面ADE,
∴三棱锥B-ADE的体积VB-ADE=$\frac{1}{3}{S}_{△ADE}×AB$=$\frac{1}{3}×(\frac{1}{2}×\sqrt{4-1}×1)×2$=$\frac{\sqrt{3}}{3}$,
${S}_{△BDE}=\frac{1}{2}×DE×BE$=$\frac{1}{2}×\sqrt{4-1}×\sqrt{4+1}$=$\frac{\sqrt{15}}{2}$,
设点A到平面BDE的距离为d,
∵VA-BDE=VB-ADE,∴$\frac{1}{3}×\frac{\sqrt{15}}{2}d$=$\frac{\sqrt{3}}{3}$,解得d=$\frac{2\sqrt{5}}{5}$,
∴点A到平面BDE的距离为$\frac{2\sqrt{5}}{5}$.
点评 本题考查线面平行的证明,考查线面垂直的证明,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| 中学 | 甲 | 乙 | 丙 | 丁 |
| 人数 | 30 | 40 | 20 | 10 |
(Ⅰ)问甲、乙、丙、丁四所中学各抽取多少名学生?
(Ⅱ)从参加问卷调查的30名学生中随机抽取2名,求这2名学生来自同一所中学的概率;
(Ⅲ)在参加问卷调查的30名学生中,从来自甲、丙两所中学的学生中随机抽取2名,用X表示抽得甲中学的学生人数,求X的分布列.
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | -$\frac{2\sqrt{2}}{3}$ |
| A. | ±$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |