题目内容
已知集合A={1,2a},B={a,b},若A∩B={
},则A∪B=( )
| 1 |
| 2 |
A、{-1,
| ||
B、{1,
| ||
C、{-1,
| ||
D、{1,
|
考点:并集及其运算
专题:集合
分析:根据集合关系即可得到结论.
解答:
解:∵A∩B={
},
∴2a=
,解得a=-1,则B={-1,b},
则b=
,即B={-1,
},
则A∪B={-1,
,1},
故选:C
| 1 |
| 2 |
∴2a=
| 1 |
| 2 |
则b=
| 1 |
| 2 |
| 1 |
| 2 |
则A∪B={-1,
| 1 |
| 2 |
故选:C
点评:本题主要考查集合的基本运算,比较基础.

练习册系列答案
相关题目
在数列{an}中,若a1=-2,且对任意的n∈N*有2an+1-2an=1,则数列{an}前15项的和为( )
A、
| ||
| B、30 | ||
| C、5 | ||
D、
|
命题“?k>0,使得直线y=kx-2的图象经过第一象限”的否定是( )
| A、?k>0,使得直线y=kx-2的图象不经过第一象限 |
| B、?k≤0,使得直线y=kx-2的图象经过第一象限 |
| C、?k>0,使得直线y=kx-2的图象不经过第一象限 |
| D、?k≤0,使得直线y=kx-2的图象不经过第一象限 |
已知cosαcosβ-sinαsinβ=0,那么sinαcosβ+cosαsinβ的值为(
| A、-1 | B、0 | C、1 | D、±1 |
 已知函数
已知函数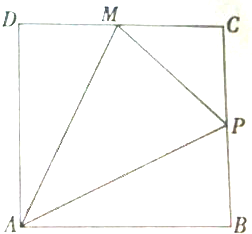 如图,动点P在边长为1的正方形ABCD上运动,点M为CD的中点,当点P沿A→B→C→M运动时,点P经过的路程设为x,△APM的面积为f(x),求f(x)的解析式.
如图,动点P在边长为1的正方形ABCD上运动,点M为CD的中点,当点P沿A→B→C→M运动时,点P经过的路程设为x,△APM的面积为f(x),求f(x)的解析式.