题目内容
3.已知f(x)是奇函数,当x>0时,f(x)=1gx,设a=f(3),b=$f(\frac{1}{4})$,c=f(-2),则( )| A. | a>c>b | B. | a>b>c | C. | c>a>b | D. | b>a>c |
分析 f(x)是奇函数,当x>0时,f(x)=1gx,结合对数函数的单调性,即可得出结论.
解答 解:∵f(x)是奇函数,当x>0时,f(x)=1gx,
∴a=f(3)=lg3,b=$f(\frac{1}{4})$=-lg4,c=f(-2)=-f(2)=-lg2,
∵lg3>-lg2>-lg4,
∴a>c>b,
故选A.
点评 本题考查了函数的奇偶性、函数的单调性,还考查了化归转化的数学思想和分析问题解决问题的能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知集合A={x||x-2|≤1},且A∩B=∅,则集合B可能是( )
| A. | {2,5} | B. | {x|x2≤1} | C. | (1,2) | D. | (-∞,-1) |
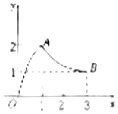 如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则$f[{\frac{1}{f(3)}}]$的值等于2.
如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则$f[{\frac{1}{f(3)}}]$的值等于2.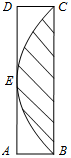 如图所示矩形ABCD边长AB=1,AD=4,抛物线顶点为边AD的中点E,且B,C两点在抛物线上,则从矩形内任取一点落在抛物线与边BC围成的封闭区域(包含边界上的点)内的概率是$\frac{2}{3}$.
如图所示矩形ABCD边长AB=1,AD=4,抛物线顶点为边AD的中点E,且B,C两点在抛物线上,则从矩形内任取一点落在抛物线与边BC围成的封闭区域(包含边界上的点)内的概率是$\frac{2}{3}$.