题目内容
4.在平面直角坐标系中,设A、B、C是曲线y=$\frac{1}{x-1}$上三个不同的点,且D、E、F分别为BC、CA、AB的中点,则过D、E、F三点的圆一定经过定点(1,0).分析 曲线y=$\frac{1}{x-1}$的对称中心为(1,0),取过对称中心直线与曲线交于A,B,A,B中点为对称中心(1,0),即可得出结论.
解答 解:曲线y=$\frac{1}{x-1}$的对称中心为(1,0),取过对称中心直线与曲线交于A,B,A,B中点为对称中心(1,0),
∴过D、E、F三点的圆一定经过定点(1,0).
故答案为(1,0).
点评 本题考查圆的方程,考查学生的计算能力,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.若执行如图所示程序框图,则输出的s值为( )


| A. | -2016 | B. | 2016 | C. | -2017 | D. | 2017 |
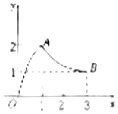 如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则$f[{\frac{1}{f(3)}}]$的值等于2.
如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则$f[{\frac{1}{f(3)}}]$的值等于2.