题目内容

5．与双曲线$C：\frac{x^2}{16}-\frac{y^2}{9}=1$有相同的渐近线的双曲线E的离心率为（　　）
A．$\frac{5}{3}$B．$\frac{5}{4}$C．$\frac{5}{3}$或$\frac{5}{4}$D．$\frac{5}{3}$或$\frac{5}{3}$

分析 求出双曲线的渐近线方程，然后求解双曲线的离心率即可．

解答 解：与双曲线$C：\frac{x^2}{16}-\frac{y^2}{9}=1$有相同的渐近线的双曲线E的渐近线方程为：$\frac{x}{4}±\frac{9}{3}=0$，
可得双曲线的焦点坐标在x轴时，离心率为：$\frac{c}{a}$=$\frac{\sqrt{16+9}}{4}$=$\frac{5}{4}$．
双曲线的焦点坐标在y轴时，离心率为：$\frac{c}{a}$=$\frac{\sqrt{9+16}}{3}$=$\frac{5}{3}$．
故选：C．

点评 本题考查双曲线的简单性质的应用，考查计算能力．

练习册系列答案
相关题目
15．已知△ABC的三个内角A，B，C的对边分别为a，b，c．
（Ⅰ）若C=2B，求证：cosA=3cosB-4cos3B；
（Ⅱ）若bsinB-csinC=a，且△ABC的面积S=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{4}$，求角B．
16．函数f（x）=lnx-mx
（Ⅰ）若曲线y=f（x）过点P（1，-1），求曲线y=f（x）在点P处的切线方程；
（Ⅱ）求函数y=f（x）在区间[1，e]上的最大值；
（Ⅲ）若x∈[1，e]，求证：lnx＜$\frac{x}{2}$．
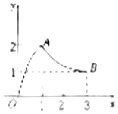13．如图，函数f（x）的图象是曲线OAB，其中点O，A，B的坐标分别为（0，0），（1，2），（3，1），则$f[{\frac{1}{f（3）}}]$的值等于2．
20．已知函数f（x）=ex（x2+x+a）在（0，f（0））处的切线与直线2x-y-3=0平行，其中a∈R．
（1）求a的值；
（2）求函数f（x）在区间[-2，2]上的最值．
10．已知a∈R，函数$f（x）=\frac{1}{{{2^x}-a}}$．
（1）当a=0时，解不等式f（x）＞1；
（2）当a＞0时，求函数y=2f（x）-f（2x）的零点个数；
（3）设a＜0，若对于t∈R，函数在区间[t，t+1]上的最大值与最小值之差都不超过1，求实数a的取值范围．
17．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，且经过点（0，1）．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）已知直线l：y=kx+m（k≠0）与椭圆C相交于A，B两点，若以AB为直径的圆过椭圆C的右顶点．求证：直线l过定点，并求出该定点的坐标．
14．已知函数$f（x）=\sqrt{3}sin2x-2{cos^2}x$．
（1）若$β∈[{0，\frac{π}{2}}]$，求f（β）的取值范围；
（2）若$tanα=2\sqrt{3}$，求f（α）的值．
15．已知集合A={x||x-2|≤1}，且A∩B=∅，则集合B可能是（　　）
A．{2，5}B．{x|x2≤1}C．（1，2）D．（-∞，-1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网