题目内容
已知|
|=1,|
|=
,
•
=0,点C在∠AOB内,且∠AOC=60°,设
=m
+n
(m,n∈R),则
=( )
| OA |
| OB |
| 3 |
| OA |
| OB |
| OC |
| OA |
| OB |
| m |
| n |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
考点:平面向量的基本定理及其意义
专题:计算题,平面向量及应用
分析:依题意建立直角坐标系,加上点C在∠AOB内的限制,可得点C的坐标,在直角三角形中由正切函数的定义可求解.
解答:
解:因为
•
=0,所以
⊥
,故可建立直角坐标系,则
=(1,0),
=(0,
),
故
=m
+n
=m(1,0)+n(0,
)=(m,
n),
又点C在∠AOB内,且∠AOC=60°,
所以tan60°=
,
所以
=1
故选:D.
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| 3 |
故
| OC |
| OA |
| OB |
| 3 |
| 3 |
又点C在∠AOB内,且∠AOC=60°,
所以tan60°=
| ||
| m |
所以
| m |
| n |
故选:D.
点评:本题为向量的基本运算,建立直角坐标系,利用坐标解决问题是一种非常有效的方法,属基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
如图是一组有规律的图案,第(1)个图案由4个基础图形组成,第(2)个图案由7个基础图形组成,…,第(670)个图案中的基础图形个数有( )


| A、2008 | B、2009 |
| C、2010 | D、2011 |
下列关于命题的说法错误的是( )
| A、命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” |
| B、命题“?x∈(-∞,0),2x<3x”是真命题 |
| C、“a=2”是“函数f(x)=logax在区间(0,+∞)上为增函数”的充分不必要条件 |
| D、若命题p:?n∈N,2n>1000,则¬p:?n∈N,2n≤1000 |
设a>1,b>1,且a≠b,令P=lg
,Q=
,则( )
| a+b |
| 2 |
| lga+lgb |
| 2 |
| A、P<Q | B、P=Q |
| C、P>Q | D、P与Q的大小不确定 |
设x,y满足约束条件
,则z=3x+y的最小值为( )
|
| A、-10 | B、-8 | C、2 | D、7 |
不等式x2-3x≤0的解集是( )
| A、{x|0<x≤3} |
| B、{x|0≤x<3} |
| C、{x|0≤x≤3} |
| D、{x|x≤0或x≥3} |
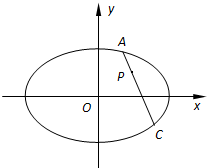 如图所示,在平面直角坐标系xOy中,过椭圆E:
如图所示,在平面直角坐标系xOy中,过椭圆E: