题目内容
已知直线
=
+1与圆x2+y2=100有公共点，且公共点的横坐标和纵坐标均为整数，那么这样的直线共有（ ）
| y |
| b |
| kx |
| b |
| A、60条 | B、66条 |
| C、70条 | D、71条 |
考点：直线与圆的位置关系
专题：计算题,直线与圆
分析：直线是截距式方程，因而不平行坐标轴，不过原点，考查圆上横坐标和纵坐标均为整数的点的个数，结合排列组合知识分类解答．
解答：
解：可知直线的横、纵截距都不为零，即与坐标轴不垂直，不过坐标原点，而圆x2+y2=100上的整数点共有12个，分别为（6，±8），（-6，±8），（8，±6），（-8，±6），（±10，0），（0，±10），前8个点中，过任意一点的圆的切线满足，有8条；12个点中过任意两点，构成C122=66条直线，其中有4条直线垂直x轴，有4条直线垂直y轴，还有6条过原点（圆上点的对称性），故满足题设的直线有52条．综上可知满足题设的直线共有52+8=60条，
故选A．
故选A．
点评：本题主要考查直线与圆的概念，以及组合的知识，既要数形结合，又要分类考虑，要结合圆上点的对称性来考虑过点的直线的特征．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
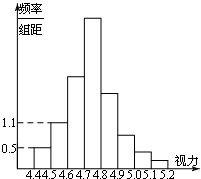为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图，由于不慎将部分数据丢失，但知道后5组的频数成等比数列，设视力在4.6到4.9之间的学生数为a，最大频率为b，则a，b的值分别为（ ）| A、77，0.53 |
| B、70，0.32 |
| C、77，5.3 |
| D、70，3.2 |
下列有关命题的说法正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题为“若x2=1，则x≠1” |
| B、“x=-1”是“x2-2x-3=0”的必要不充分条件 |
| C、命题“?x∈R使得x2+x-1＜0”的否定是“?x∈R，均有x2+x-1＞0” |
| D、命题“已知x，y∈R，若x+y≠5，则x≠1或y≠4”为真命题 |
