题目内容
下列命题中：
①若
•
=0，则
=
或
=
；
②若不平行的两个非零向量
，
满足|
|=|
|，则(
+
)•(
-
)=0；
③若
与
平行，则|
•
|=|
|•|
|；
④若
∥
，
∥
，则
∥
；
其中假命题的个数是（ ）
①若
| a |
| b |
| a |
| 0 |
| b |
| 0 |
②若不平行的两个非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
③若
| a |
| b |
| a |
| b |
| a |
| b |
④若
| a |
| b |
| b |
| c |
| a |
| c |
其中假命题的个数是（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：命题的真假判断与应用
专题：简易逻辑
分析：利用数量积判断①的正误；
通过向量的模相等，判断②中(
+
)•(
-
)=0的真假即可；
利用向量平行判断③的正误；
通过向量共线判断④的正误．
通过向量的模相等，判断②中(
| a |
| b |
| a |
| b |
利用向量平行判断③的正误；
通过向量共线判断④的正误．
解答：
解：①若
•
=0，则
=
或
=
或
⊥
；故本命题不正确．
②若不平行的两个非零向量
，
满足|
|=|
|，则有
2=
2
既有
2-
2=(
+
)•(
-
)=0；故本命题正确．
③若
与
平行，则有两个向量的夹角是0或π，∵|
×
|=|
||
|cosθ，∴|
×
|=|
||
|，故本命题正确．
④当
=0时，一定有若
∥
，
∥
，但是
∥
不一定成立；故本命题不正确．
故选：B．
| a |
| b |
| a |
| 0 |
| b |
| 0 |
| a |
| b |
②若不平行的两个非零向量
| a |
| b |
| a |
| b |
| a |
| b |
既有
| a |
| b |
| a |
| b |
| a |
| b |
③若
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
④当
| b |
| a |
| b |
| b |
| c |
| a |
| c |
故选：B．
点评：本题主要考察命题的真假判断与应用，属于基础题．
练习册系列答案
星级口算天天练系列答案
相关题目
设an=（n+1）2，bn=n2-n（n∈N*），则下列命题中不正确的是（ ）
| A、{an+1-an}是等差数列 |
| B、{bn+1-bn}是等差数列 |
| C、{an-bn}是等差数列 |
| D、{an+bn}是等差数列 |
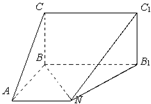如图五面体中，四边形CBB1C1为矩形，B1C1⊥平面ABB1N，四边形ABB1N为梯形，且AB⊥BB1，BC=AB=AN=
| 1 |
| 2 |
（1）求证：BN⊥平面C1B1N；
（2）求此五面体的体积．
设F1，F2是椭圆
+
=1的两个焦点，点M在椭圆上，若△MF1F2是直角三角形，则△MF1F2的面积等于（ ）
| x2 |
| 25 |
| y2 |
| 16 |
A、
| ||
B、
| ||
| C、16 | ||
D、
|
已知坐标满足方程F（x，y）=0的点都在曲线C上，那么（ ）
| A、曲线C上的点的坐标都适合方程F（x，y）=0 |
| B、凡坐标不适合F（x，y）=0的点都不在C上 |
| C、不在C上的点的坐标不必适合F（x，y）=0 |
| D、不在C上的点的坐标有些适合F（x，y）=0，有些不适合F（x，y）=0 |