题目内容
1.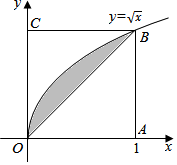 如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好取自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)=$\frac{1}{4}$.
如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好取自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)=$\frac{1}{4}$.
分析 阴影部分由函数y=x与$y=\sqrt{x}$围成,由定积分公式,计算可得阴影部分的面积,进而由几何概型公式计算可得答案.
解答 解:根据题意,阴影部分由函数y=x与$y=\sqrt{x}$围成,其面积为${∫}_{0}^{1}$($\sqrt{x}$-x)dx=($\frac{2}{3}{x}^{\frac{3}{2}}-\frac{{x}^{2}}{2}$)${|}_{0}^{1}$=$\frac{1}{6}$,
A表示事件“点P恰好取自曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,面积为$\frac{1}{6}$+$\frac{1}{2}$=$\frac{2}{3}$,
则P(B|A)等于$\frac{\frac{1}{6}}{\frac{2}{3}}$=$\frac{1}{4}$.
故答案为$\frac{1}{4}$.
点评 本题考查几何概型的计算,涉及定积分在求面积中的应用,关键是正确计算出阴影部分的面积.

练习册系列答案
相关题目
11.已知集合A={0,1,2},B={x|x2-5x+4<0},A∩(∁RB)=( )
| A. | {0,1,2} | B. | {1,2} | C. | {0} | D. | {0,1} |
12.抛物线y2=4x的焦点为F,点A(5,3),M为抛物线上一点,且M不在直线AF上,则△MAF周长的最小值为( )
| A. | 10 | B. | 11 | C. | 12 | D. | 6+$\sqrt{29}$ |
6.已知三个向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$共面,且均为单位向量,$\overrightarrow{a}$•$\overrightarrow{b}$=0,则|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|的取值范围是( )
| A. | [$\sqrt{2}$-1,$\sqrt{2}$+1] | B. | [1,$\sqrt{2}$] | C. | [$\sqrt{2}$,$\sqrt{3}$] | D. | [$\sqrt{2}$-1,1] |
13.设sin(π-θ)=$\frac{1}{3}$,则cos2θ=( )
| A. | ±$\frac{4\sqrt{2}}{9}$ | B. | $\frac{7}{9}$ | C. | -$\frac{4\sqrt{2}}{9}$ | D. | -$\frac{7}{9}$ |
10.“ln(x+2)<0”是“x<0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
11.(1+x)6(1+y)4的展开式中,记xmyn项的系数为f(m,n),则f(3,0)+f(0,3)=( )
| A. | 9 | B. | 16 | C. | 18 | D. | 24 |