题目内容
6.已知三个向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$共面,且均为单位向量,$\overrightarrow{a}$•$\overrightarrow{b}$=0,则|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|的取值范围是( )| A. | [$\sqrt{2}$-1,$\sqrt{2}$+1] | B. | [1,$\sqrt{2}$] | C. | [$\sqrt{2}$,$\sqrt{3}$] | D. | [$\sqrt{2}$-1,1] |
分析 根据题意,可设$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),$\overrightarrow{c}$=(x,y),得|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|=$\sqrt{{(x-1)}^{2}{+(y-1)}^{2}}$,结合图形求出它的最大、最小值.
解答 解:三个向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$共面,且均为单位向量,$\overrightarrow{a}$•$\overrightarrow{b}$=0,
可设$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),$\overrightarrow{c}$=(x,y),
则$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$=(1-x,1-y),|$\overrightarrow{c}$|=$\sqrt{{x}^{2}{+y}^{2}}$=1;
∴|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|=$\sqrt{{(1-x)}^{2}{+(1-y)}^{2}}$=$\sqrt{{(x-1)}^{2}{+(y-1)}^{2}}$,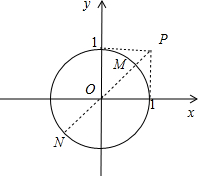
它表示单位圆上的点到定点P(1,1)的距离,
其最大值是PM=r+|OP|=1+$\sqrt{2}$,最小值是|OP|-r=$\sqrt{2}$-1,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|的取值范围是[$\sqrt{2}$-1,$\sqrt{2}$+1].
故选:A.
点评 本题考查了向量的垂直与数量积的关系、数量积的运算性质、点与圆上的点的距离大小关系,考查了推理能力和计算能力,是中档题.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案①对任意的x1,x2∈[4,8],当x1<x2时,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0;
②f(x+4)=-f(x);
③y=f(x+4)是偶函数;
若a=f(6),b=f(11),c=f(2017),则a,b,c的大小关系正确的是( )
| A. | a<b<c | B. | b<a<c | C. | a<c<b | D. | c<b<a |
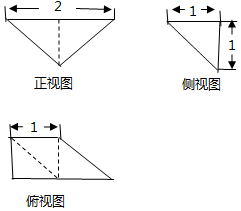 某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )
某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )| A. | $\frac{1}{2}c{m^3}$ | B. | 1cm3 | C. | $\frac{3}{2}c{m^3}$ | D. | 3cm3 |
| A. | (0,2) | B. | (0,$\frac{{e}^{2}}{4}$) | C. | (0,e) | D. | (0,+∞) |
| A. | [-1,$\frac{1}{4}$] | B. | [$\frac{1}{4}$,1] | C. | [-2,$\frac{1}{4}$] | D. | [$\frac{1}{3}$,1] |
| A. | -240 | B. | 240 | C. | -160 | D. | 160 |
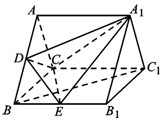 如图,在三棱柱ABC-A1B1C1中,底面△ABC是等边三角形,且AA1⊥平面ABC,D为AB的中点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是等边三角形,且AA1⊥平面ABC,D为AB的中点.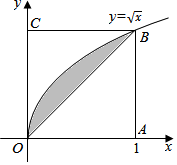 如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好取自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)=$\frac{1}{4}$.
如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好取自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)=$\frac{1}{4}$.