题目内容
12.抛物线y2=4x的焦点为F,点A(5,3),M为抛物线上一点,且M不在直线AF上,则△MAF周长的最小值为( )| A. | 10 | B. | 11 | C. | 12 | D. | 6+$\sqrt{29}$ |
分析 求△MAF周长的最小值,即求|MA|+|MF|的最小值.设点M在准线上的射影为D,则根据抛物线的定义,可知|MF|=|MD|,因此问题转化为求|MA|+|MD|的最小值,根据平面几何知识,当D、M、A三点共线时|MA|+|MD|最小,由此即可求出|MA|+|MF|的最小值.
解答 解:求△MAF周长的最小值,即求|MA|+|MF|的最小值,
设点M在准线上的射影为D,
根据抛物线的定义,可知|MF|=|MD|
因此,|MA|+|MF|的最小值,即|MA|+|MD|的最小值
根据平面几何知识,可得当D,M,A三点共线时|MA|+|MD|最小,
因此最小值为xA-(-1)=5+1=6,
∵|AF|=$\sqrt{(5-1)^{2}+(3-0)^{2}}$=5,
∴△MAF周长的最小值为11,
故选B.
点评 考查椭圆的定义、标准方程,以及简单性质的应用,判断当D,M,A三点共线时|MA|+|MD|最小,是解题的关键.

练习册系列答案
相关题目
2.如图,在△ABC中,点D满足$\overrightarrow{AD}$+2$\overrightarrow{BD}$=0,$\overrightarrow{CD}$•$\overrightarrow{AC}$=0,且|$\overrightarrow{CA}$+$\overrightarrow{AD}$|=2,则$\overrightarrow{DC}$•$\overrightarrow{CB}$=( )
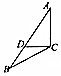

| A. | -6 | B. | 6 | C. | 2 | D. | -$\frac{8}{3}$ |
4.在区间[0,8]上随机取一个x的值,执行如图的程序框图,则输出的y≥3的概率为( )


| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
2.已知集合M={-1,0,1,2,3},N={x|x2-2x>0},则M∩N=( )
| A. | {3} | B. | {2,3} | C. | {-1,3} | D. | {0,1,2} |
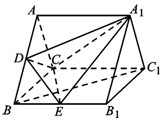 如图,在三棱柱ABC-A1B1C1中,底面△ABC是等边三角形,且AA1⊥平面ABC,D为AB的中点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是等边三角形,且AA1⊥平面ABC,D为AB的中点.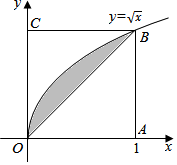 如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好取自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)=$\frac{1}{4}$.
如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好取自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)=$\frac{1}{4}$.