题目内容

11．已知集合A={0，1，2}，B={x|x2-5x+4＜0}，A∩（∁RB）=（　　）
A．{0，1，2}B．{1，2}C．{0}D．{0，1}

分析 解不等式得集合B，根据补集与交集的定义写出A∩（∁RB）．

解答 解：集合A={0，1，2}，
B={x|x2-5x+4＜0}={x|1＜x＜4}，
∴∁RB={x|x≤1或x≥4}，
∴A∩（∁RB）={0，1}．
故选：D．

点评 本题考查了解不等式与集合的运算问题，是基础题．

练习册系列答案
相关题目
1．直角坐标平面上一机器人在行进中始终保持到两点A（a，0）和B（0，1）的距离相等，且机器人也始终接触不到直线L：y=x+1，则a的值为1．
2．如图，在△ABC中，点D满足$\overrightarrow{AD}$+2$\overrightarrow{BD}$=0，$\overrightarrow{CD}$•$\overrightarrow{AC}$=0，且|$\overrightarrow{CA}$+$\overrightarrow{AD}$|=2，则$\overrightarrow{DC}$•$\overrightarrow{CB}$=（　　）
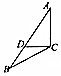
A．-6B．6C．2D．-$\frac{8}{3}$
19．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，点B是椭圆C的上顶点，点Q在椭圆C上（异于B点）．
（Ⅰ）若椭圆V过点（-$\sqrt{3}$，$\frac{\sqrt{2}}{2}$），求椭圆C的方程；
（Ⅱ）若直线l：y=kx+b与椭圆C交于B、P两点，若以PQ为直径的圆过点B，证明：存在k∈R，$\frac{|BP|}{|BQ|}$=$\frac{1}{2}$．
6．已知函数y=2sin（x+$\frac{π}{2}$）cos（x-$\frac{π}{2}$）与直线y=$\frac{1}{2}$相交，若在y轴右侧的交点自左向右依次记为M1，M2，M3，…，则|$\overrightarrow{{M}_{1}{M}_{12}}$|等于（　　）
A．$\frac{16π}{3}$B．6πC．$\frac{17π}{3}$D．12π
16．已知函数的定义域为R，且满足下列三个条件：
①对任意的x1，x2∈[4，8]，当x1＜x2时，都有$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＞0；
②f（x+4）=-f（x）；
③y=f（x+4）是偶函数；
若a=f（6），b=f（11），c=f（2017），则a，b，c的大小关系正确的是（　　）
A．a＜b＜cB．b＜a＜cC．a＜c＜bD．c＜b＜a
3．已知动点P到点（$\frac{1}{2}$，0）的距离比它到直线x=-$\frac{5}{2}$的距离小2．
（Ⅰ）求动点P的轨迹方程；
（Ⅱ）记P点的轨迹为E，过点S（2，0）斜率为k1的直线交E于A，B两点，Q（1，0），延长AQ，BQ与E交于C，D两点，设CD的斜率为k2，证明：$\frac{{k}_{2}}{{k}_{1}}$为定值．
20．对于定义域为D的函数y=f（x），如果存在区间[m，n]⊆D，其中m＜n，同时满足：①f（x）在[m，n]内是单调函数；②当定义域是[m，n]时，f（x）的值域也是[m，n]．
则称函数f（x）是区间[m，n]上的“保值函数”，区间[m，n]称为“保值区间”．
（1）求证：函数g（x）=x2-2x不是定义域[0，1]上的“保值函数”．
（2）若函数f（x）=2+$\frac{1}{a}$-$\frac{1}{{a}^{2}x}$（a∈R，a≠0）是区间[m，n]上的“保值函数”，求a的取值范围．
（3）对（2）中函数f（x），若不等式|a2f（x）|≤2x对x≥1恒成立，求实数a的取值范围．
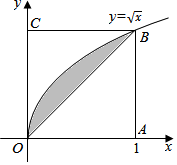1．如图所示，在边长为1的正方形OABC内任取一点P，用A表示事件“点P恰好取自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”，B表示事件“点P恰好取自阴影部分内”，则P（B|A）=$\frac{1}{4}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网