题目内容
4.已知正方形ABCD的边长为2,边AB,CD分别为圆柱上下底面的直径,若一蚂蚁从点A沿圆柱的表面爬到点C,则该蚂蚁所走的最短路程为$\sqrt{{π^2}+4}$.分析 沿母线AD剪开再展开,则蚂蚁所走的最短路程为右图中直线段AC的长,由圆的周长公式求出BC,再由勾股定理求得答案.
解答 解:如图,
圆的底面半径为r=1,半圆周长为π,AB=2,
∴蚂蚁所走的最短路程为AC=$\sqrt{{π}^{2}+4}$.
故答案为:$\sqrt{{π^2}+4}$.
点评 本题考查旋转体表面上的最短距离问题,考查空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
9.函数f(x)=$\sqrt{1-x}$-$\sqrt{x}$的定义域为( )
| A. | [0,1] | B. | (0,1] | C. | (0,1) | D. | (-1,0) |
13.参数方程$\left\{{\begin{array}{l}{x={{cos}^2}θ}\\{y={{sin}^2}θ}\end{array}}\right.$(θ为参数)表示的曲线是( )
| A. | 直线 | B. | 圆 | C. | 线段 | D. | 射线 |
14.某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金不超过54万元,假设种植黄瓜和韭菜的产量、成本和售价如表:
则一年的种植总利润(总利润=总销售收入-总种植成本最大值为45万元.
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 5吨 | 0.9万元 | 0.3万元 |
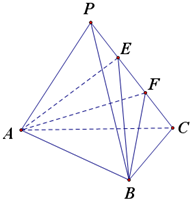 在三棱锥P-ABC中,PA=PB=PC=3,AB=$\sqrt{6}$,BC=$\sqrt{3}$,AB⊥BC,E,F为PC的三等分点.
在三棱锥P-ABC中,PA=PB=PC=3,AB=$\sqrt{6}$,BC=$\sqrt{3}$,AB⊥BC,E,F为PC的三等分点.