题目内容
定义函数f(k)表示k的最大奇因数,例如:f(1)=1,f(2)=1,f(3)=3,f(4)=1.
(1)f(1)+f(3)+f(5)+…+f(2n-1)= .
(2)f(1)+f(2)+f(3)+…+f(2n)= .
(1)f(1)+f(3)+f(5)+…+f(2n-1)=
(2)f(1)+f(2)+f(3)+…+f(2n)=
考点:进行简单的合情推理
专题:计算题,等差数列与等比数列,推理和证明
分析:(1)由题意,f(1)+f(3)+f(5)+…+f(2n-1)=1+3+5+…+2n-1=n2,
(2)记Sn=f(1)+f(2)+f(3)+…+f(2n),从而可推出Sn=4n-1+Sn-1,从而求出Sn-Sn-1=4n-1;从而可得Sn=(Sn-Sn-1)+(Sn-1-Sn-2)+…+(S2-S1)+S1=4n-1+4n-2+4n-3+…+4+2=
4n+
.
(2)记Sn=f(1)+f(2)+f(3)+…+f(2n),从而可推出Sn=4n-1+Sn-1,从而求出Sn-Sn-1=4n-1;从而可得Sn=(Sn-Sn-1)+(Sn-1-Sn-2)+…+(S2-S1)+S1=4n-1+4n-2+4n-3+…+4+2=
| 1 |
| 3 |
| 2 |
| 3 |
解答:
解(1)由题意,f(1)+f(3)+f(5)+…+f(2n-1)=1+3+5+…+2n-1=n2,
(2)记Sn=f(1)+f(2)+f(3)+…+f(2n),
则Sn-1=f(1)+f(2)+f(3)+…+f(2n-1);
Sn=f(1)+f(2)+f(3)+…+f(2n)
=f(1)+f(3)+…+f(2n-1)+[f(2)+f(4)+…+f(2n)]
=1+3+5+…+2n-1+[f(1)+f(2)+f(3)+…+f(2n-1)]
=4n-1+Sn-1,
故Sn-Sn-1=4n-1;
则Sn=(Sn-Sn-1)+(Sn-1-Sn-2)+…+(S2-S1)+S1
=4n-1+4n-2+4n-3+…+4+2
=
4n+
.
故答案为:n2,
4n+
.
(2)记Sn=f(1)+f(2)+f(3)+…+f(2n),
则Sn-1=f(1)+f(2)+f(3)+…+f(2n-1);
Sn=f(1)+f(2)+f(3)+…+f(2n)
=f(1)+f(3)+…+f(2n-1)+[f(2)+f(4)+…+f(2n)]
=1+3+5+…+2n-1+[f(1)+f(2)+f(3)+…+f(2n-1)]
=4n-1+Sn-1,
故Sn-Sn-1=4n-1;
则Sn=(Sn-Sn-1)+(Sn-1-Sn-2)+…+(S2-S1)+S1
=4n-1+4n-2+4n-3+…+4+2
=
| 1 |
| 3 |
| 2 |
| 3 |
故答案为:n2,
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题考查了合情推理的应用及等差、等比数列的应用,属于中档题.

练习册系列答案
相关题目
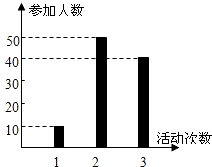 某校高一学生积极参加社会公益活动,成立了公益社,公益社共100人,据统计,他们在今年三月参加公益活动的次数统计如图所示,
某校高一学生积极参加社会公益活动,成立了公益社,公益社共100人,据统计,他们在今年三月参加公益活动的次数统计如图所示,