题目内容
已知
=（sinx，cosx），
=（cosx，cosx），x∈R，f（x）=
•（
+
）．
（1）求f（x）的解析式；
（2）求f（x）在[-
，
]上的最大值，最小值；
（3）若f（x）=
+
，求sin4x．
| a |
| b |
| a |
| a |
| b |
（1）求f（x）的解析式；
（2）求f（x）在[-
| π |
| 4 |
| π |
| 4 |
（3）若f（x）=
3
| ||
| 10 |
| 3 |
| 2 |
考点：平面向量数量积的运算,三角函数中的恒等变换应用
专题：平面向量及应用
分析：运用向量的坐标运算得到f（x），然后化简为最简形式，依据三角函数性质解答．
解答：
解：（1）由已知，
=（sinx，cosx），
=（cosx，cosx），x∈R，所以f（x）=
•（
+
）=sinx（sinx+cosx）+2cos2x=
sin（2x+
）+
；
（2）由（1）得，f（x）═
sin（2x+
）+
，x∈[-
，
]，2x+
∈[-
，
]，
所以f（x）在[-
，
]上的最大值为f（
）=
+
，最小值为f（-
）=
×(-
)+
=1；
（3）f（x）=
+
=
sin（2x+
）+
，所以sin（2x+
）=
，sin4x=-cos（4x+
）=-1+2sin2（2x+
）=-1+2×
=
．
| a |
| b |
| a |
| a |
| b |
| ||
| 2 |
| π |
| 4 |
| 3 |
| 2 |
（2）由（1）得，f（x）═
| ||
| 2 |
| π |
| 4 |
| 3 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
所以f（x）在[-
| π |
| 4 |
| π |
| 4 |
| π |
| 8 |
| ||
| 2 |
| 3 |
| 3 |
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
（3）f（x）=
3
| ||
| 10 |
| 3 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| 3 |
| 2 |
| π |
| 4 |
| 3 |
| 5 |
| π |
| 2 |
| π |
| 4 |
| 9 |
| 25 |
| 7 |
| 25 |
点评：本题考查了向量的坐标运算以及运用基本关系式、倍角公式等化简三角函数式，注意符号和名称．
练习册系列答案
相关题目
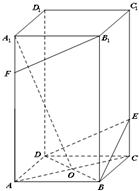如图，在正四棱柱ABCD-A1B1C1D1中，点O是正方形ABCD对角线的交点，AA1=4，AB=2，点E，F分别在CC1和A1A上，且A1F=CE
一个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得该几何体的体积是已知f（x）=
，若a，b，c，d是互不相同的四个正数，且f（a）=f（b）=f（c）=f（d），则abcd的取值范围是（ ）
|
| A、（21，25） |
| B、（21，24） |
| C、（20，24） |
| D、（20，25） |
