题目内容
若双曲线
-
=1上一点P到其左焦点的距离为5，则点P到右焦点的距离为 ．
| x2 |
| 4 |
| y2 |
| 12 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：求出双曲线的a，b，c，运用双曲线的定义，求得|PF2|=1或9，讨论P在左支和右支上，求出最小值，即可判断P的位置，进而得到所求距离．
解答：
解：双曲线
-
=1的a=2，b=2
，c=
=4，
设左右焦点为F1，F2．
则有双曲线的定义，得||PF1|-|PF2||=2a=4，
由于|PF1|=5，则有|PF2|=1或9，
若P在右支上，则有|PF2|≥c-a=2，
若P在左支上，则|PF2|≥c+a=6，
故|PF2|=1舍去；
由于|PF1|=5＜c+a=6，
则有P在左支上，则|PF2|=9．
故答案为：9
| x2 |
| 4 |
| y2 |
| 12 |
| 3 |
| a2+b2 |
设左右焦点为F1，F2．
则有双曲线的定义，得||PF1|-|PF2||=2a=4，
由于|PF1|=5，则有|PF2|=1或9，
若P在右支上，则有|PF2|≥c-a=2，
若P在左支上，则|PF2|≥c+a=6，
故|PF2|=1舍去；
由于|PF1|=5＜c+a=6，
则有P在左支上，则|PF2|=9．
故答案为：9
点评：本题考查双曲线的方程和定义，考查分类讨论的思想方法，考查运算能力，属于基础题和易错题．
练习册系列答案
阅读快车系列答案
相关题目
已知全集U=R，A={x|y=
}，则∁UA=（ ）
| 1 | ||
|
| A、[1，+∞） |
| B、（-∞，1） |
| C、（1，+∞） |
| D、（-∞，1] |
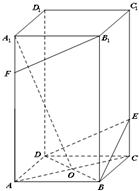如图，在正四棱柱ABCD-A1B1C1D1中，点O是正方形ABCD对角线的交点，AA1=4，AB=2，点E，F分别在CC1和A1A上，且A1F=CE
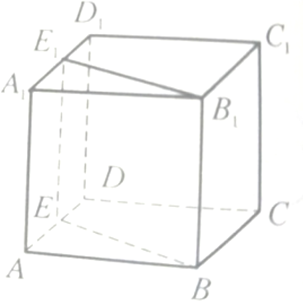经过正方体ABCD-A1B1C1D1的棱BB1作一平面交平面AA1D1D于E1E．求证：BB1∥E1E．已知f（x）=
，若a，b，c，d是互不相同的四个正数，且f（a）=f（b）=f（c）=f（d），则abcd的取值范围是（ ）
|
| A、（21，25） |
| B、（21，24） |
| C、（20，24） |
| D、（20，25） |