题目内容
某一几何体的三视图如图所示,其中圆的半径都为1,则该几何体的体积为 .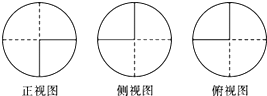

考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:几何体是球切去两个
球体,根据球的半径为1,代入球的体积公式计算.
| 1 |
| 8 |
解答:
解:由三视图知:几何体是球切去两个
球体,
球的半径为1,∴球的体积为
π×13=
π,
∴几何体的体积V=
π×(1-2×
)=π.
故答案为:π.
| 1 |
| 8 |
球的半径为1,∴球的体积为
| 4 |
| 3 |
| 4 |
| 3 |
∴几何体的体积V=
| 4 |
| 3 |
| 1 |
| 8 |
故答案为:π.
点评:本题考查了由三视图求几何体的体积,根据三视图判断几何体的形状及结构特征是关键.

练习册系列答案
相关题目
若sin(α+
)=
,则sin2α等于( )
| π |
| 4 |
| ||
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx,设a=f(
),b=f(
),c=f(
),则( )
| 4 |
| 3 |
| 3 |
| 2 |
| 5 |
| 2 |
| A、a<b<c |
| B、b<a<c |
| C、c<b<a |
| D、c<a<b |
若[x]表示不超过x的最大整数,执行如图所示的程序框图,则输出的S值为( )

| A、4 | B、5 | C、7 | D、9 |
已知函数y=2sin(x-
)cos(x-
)+2cos2(x+
)-1,则函数的最小正周期T和它的图象上的一条对称轴方程分别是( )
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
A、T=2π,x=
| ||
B、T=2π,x=
| ||
C、T=π,x=
| ||
D、T=π,x=
|