题目内容
16.在平面四边形ABCD中,∠A=45°,∠B=120°,AB=$\sqrt{2}$,AD=2.设CD=t,则t的取值范围是[$\frac{\sqrt{2}}{2}$,1+$\sqrt{3}$).分析 在△ABD中,由余弦定理得DB=$\sqrt{2}$,即$∠ABD=\frac{π}{2}$.$∠DBC=\frac{π}{6}$,点C在射线BT上运动(如图),要使ABCD为平面四边形ABCD,当DC⊥BT时,CD最短,为$\frac{\sqrt{2}}{2}$,当A,D,C共线时,如图,在△ABC2中,由正弦定理可得$A{C}_{2}=3+\sqrt{3}$,$D{C}_{2}=1+\sqrt{3}$.即可得到答案.
解答 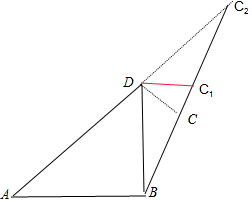 解:在△ABD中,∵∠A=45°,∠B=120°,AB=$\sqrt{2}$,AD=2,
解:在△ABD中,∵∠A=45°,∠B=120°,AB=$\sqrt{2}$,AD=2,
由余弦定理得BD2=AD2+AB2-2AD•ABcosA=2.
∴DB=$\sqrt{2}$,即△ABD为等腰直角三角形,$∠ABD=\frac{π}{2}$.
∴$∠DBC=\frac{π}{6}$,
所以点C在射线BT上运动(如图),要使ABCD为平面四边形ABCD,
当DC⊥BT时,CD最短,为$\frac{\sqrt{2}}{2}$,
当A,D,C共线时,如图,在△ABC2中,由正弦定理可得$\frac{A{C}_{2}}{sin12{0}^{0}}=\frac{AB}{sin1{5}^{0}}$
解得$A{C}_{2}=3+\sqrt{3}$,$D{C}_{2}=1+\sqrt{3}$.
∴设CD=t,则t的取值范围是[$\frac{\sqrt{2}}{2}$,1+$\sqrt{3}$),
故答案为:$[{\frac{{\sqrt{2}}}{2},\sqrt{3}+1})$.
点评 本题考查了正余弦定理的应用,动点问题的极端化处理是解题的关键,属于中档题.

练习册系列答案
相关题目
6.已知公比q≠1的等比数列{an}前n项和Sn,a1=1,S3=3a3,则S5=( )
| A. | 1 | B. | 5 | C. | $\frac{31}{48}$ | D. | $\frac{11}{16}$ |
4.已知集合A={x|y=lg(x+1)},B={-2,-1,0,1},则(∁RA)∩B=( )
| A. | {-2,-1} | B. | {-2} | C. | {-1,0,1} | D. | {0,1} |
11.已知函数f(x)=|lnx|,$g(x)=\left\{\begin{array}{l}0,0<x≤1\\|{x^2}-4|-2,x>1\end{array}\right.$若方程|f(x)+g(x)|=a有4个实根,则a的取值范围是( )
| A. | (0,1] | B. | (0,2-ln2) | C. | [1,2-ln2] | D. | [1,2-ln2) |
1.在平面直角坐标系xOy中,以(-2,0)为圆心且与直线(3m+1)x+(1-2m)y-5=0(m∈R)相切的所有圆中,面积最大的圆的标准方程是( )
| A. | (x+2)2+y2=16 | B. | (x+2)2+y2=20 | C. | (x+2)2+y2=25 | D. | (x+2)2+y2=36 |
5.已知向量$\overrightarrow{OA}=({3,1}),\overrightarrow{OB}=({-1,3})$,$\overrightarrow{OC}=m\overrightarrow{OA}-n\overrightarrow{OB}({m>0,n>0})$,若m+n=1,则$|{\overrightarrow{OC}}$|的最小值为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{10}}}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
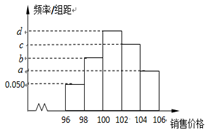 某企业市场调研部为调查新开发的产品定价与销量之间的关系,在某地区进行小范围差价试销,已知该产品定价区间为[96,106](单位:元/件),已知统计了600件产品的销售价格,其频率分布直方图如图所示,若各个小方形的高构成一个等差数列,则在这600件产品中,销售价格在区间[98,102)内的产品件数是135.
某企业市场调研部为调查新开发的产品定价与销量之间的关系,在某地区进行小范围差价试销,已知该产品定价区间为[96,106](单位:元/件),已知统计了600件产品的销售价格,其频率分布直方图如图所示,若各个小方形的高构成一个等差数列,则在这600件产品中,销售价格在区间[98,102)内的产品件数是135.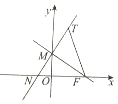 如图,在平面直角坐标中,过F(1,0)的直线FM与y轴交于点M,直线MN与直线FM垂直,且与x轴交于点N,T是点N关于直线FM的对称点.
如图,在平面直角坐标中,过F(1,0)的直线FM与y轴交于点M,直线MN与直线FM垂直,且与x轴交于点N,T是点N关于直线FM的对称点.