题目内容
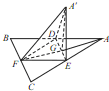 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:①平面A′FG⊥平面ABC;
②BC∥平面A′DE;
③三棱锥A′-DEF的体积最大值为
| 1 |
| 64 |
④动点A′在平面ABC上的射影在线段AF上;
⑤二面角A′-DE-F大小的范围是[0,
| π |
| 2 |
其中正确的命题是
考点:命题的真假判断与应用,棱柱、棱锥、棱台的体积,直线与平面平行的判定,二面角的平面角及求法
专题:空间位置关系与距离
分析:①由已知可得四边形ADEF是菱形,再利用菱形对角线的性质、线面面面垂直的判定与性质定理即可得出;
②由三角形中位线定理和线面平行的判定定理即可得出;
③当面A′DE⊥面ABC时,三棱锥A′-DEF的体积达到最大,再利用体积计算公式即可得出;
④由平面A′FG⊥平面ABC,利用面面垂直的性质定理可得点A′在面ABC上的射影在线段AF上;
⑤在旋转过程中二面角A′-DE-F大小的范围是[0,π],即可判断出.
②由三角形中位线定理和线面平行的判定定理即可得出;
③当面A′DE⊥面ABC时,三棱锥A′-DEF的体积达到最大,再利用体积计算公式即可得出;
④由平面A′FG⊥平面ABC,利用面面垂直的性质定理可得点A′在面ABC上的射影在线段AF上;
⑤在旋转过程中二面角A′-DE-F大小的范围是[0,π],即可判断出.
解答:
解:①由已知可得四边形ADEF是菱形,则DE⊥GA′,DE⊥GF,
∴DE⊥平面A′FG,∴平面A′FG⊥平面ABC,①正确;
②由三角形中位线定理可得BC∥DE,∴BC∥平面A′DE,∴②正确;
③当面A′DE⊥面ABC时,三棱锥A′-DEF的体积达到最大,
最大值为
×
×
a2×
a=
a3,③正确;
④由平面A′FG⊥平面ABC,可知点A′在面ABC上的射影在线段AF上,∴④正确;
⑤在旋转过程中二面角A′-DE-F大小的范围是[0,π],∴⑤不正确.
故答案为:①②③④.
∴DE⊥平面A′FG,∴平面A′FG⊥平面ABC,①正确;
②由三角形中位线定理可得BC∥DE,∴BC∥平面A′DE,∴②正确;
③当面A′DE⊥面ABC时,三棱锥A′-DEF的体积达到最大,
最大值为
| 1 |
| 3 |
| 1 |
| 4 |
| ||
| 4 |
| ||
| 4 |
| 1 |
| 64 |
④由平面A′FG⊥平面ABC,可知点A′在面ABC上的射影在线段AF上,∴④正确;
⑤在旋转过程中二面角A′-DE-F大小的范围是[0,π],∴⑤不正确.
故答案为:①②③④.
点评:本题中考查了空间线面的位置关系,熟练掌握其判定定理和性质定理是解题的关键,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目