题目内容
判断下列命题,其中正确的为
①若sinα>0,则α角的终边落在第一或第二象限;
②函数y=2x(x<1)的值域为{y|y<2};
③函数f(x)=loga
(a>0且a≠1)在定义域内是奇函数;
④sinx-cosx=
,则sin3x-cos3x=
.
①若sinα>0,则α角的终边落在第一或第二象限;
②函数y=2x(x<1)的值域为{y|y<2};
③函数f(x)=loga
| 2-sinx |
| 2+sinx |
④sinx-cosx=
| ||
| 2 |
5
| ||
| 8 |
考点:命题的真假判断与应用
专题:函数的性质及应用,三角函数的求值,三角函数的图像与性质
分析:①由正弦函数的图象与性质得出sinα>0时,α角的取值范围,即可判定命题是否正确;
②由指数函数y=2x的图象与性质得出x<1时,y=2x的值域;
③由函数的奇偶性定义判定f(x)=loga
的奇偶性即可;
④由sinx-cosx=
两边平方,求出sinxcosx的值,把sin3x-cos3x因式分解,即可计算结果.
②由指数函数y=2x的图象与性质得出x<1时,y=2x的值域;
③由函数的奇偶性定义判定f(x)=loga
| 2-sinx |
| 2+sinx |
④由sinx-cosx=
| ||
| 2 |
解答:
解:①考查正弦函数的图象知,
当sinα>0时,α角的终边落在第一、第二象限或y正半轴上,
∴命题①错误;
②考查指数函数y=2x的图象知,
当x<1时,y=2x的值域是{y|0<y<2},
∴命题②错误;
③∵函数f(x)=loga
的定义域为R,
对?x∈R,有f(-x)=loga
=loga(
)-1=-loga
=-f(x)
(其中a>0且a≠1),
∴f(x)是R上的奇函数,
∴命题③正确;
④∵sinx-cosx=
,
∴1-2sinxcosx=
,
∴sinxcosx=
,
∴sin3x-cos3x=(sinx-cosx)(sin2x+sinxcosx+cos2x)
=
×(1+
)
=
,
∴命题④正确;
所以,正确的命题是③④.
故答案为:③④.
当sinα>0时,α角的终边落在第一、第二象限或y正半轴上,
∴命题①错误;
②考查指数函数y=2x的图象知,
当x<1时,y=2x的值域是{y|0<y<2},
∴命题②错误;
③∵函数f(x)=loga
| 2-sinx |
| 2+sinx |
对?x∈R,有f(-x)=loga
| 2-sin(-x) |
| 2+sin(-x) |
| 2-sinx |
| 2+sinx |
| 2-sinx |
| 2+sinx |
(其中a>0且a≠1),
∴f(x)是R上的奇函数,
∴命题③正确;
④∵sinx-cosx=
| ||
| 2 |
∴1-2sinxcosx=
| 1 |
| 2 |
∴sinxcosx=
| 1 |
| 4 |
∴sin3x-cos3x=(sinx-cosx)(sin2x+sinxcosx+cos2x)
=
| ||
| 2 |
| 1 |
| 4 |
=
5
| ||
| 8 |
∴命题④正确;
所以,正确的命题是③④.
故答案为:③④.
点评:本题通过命题真假的判定,考查了三角函数的图象与性质,三角恒等变换以及指数函数与对数函数的问题,是综合题.

练习册系列答案
相关题目
已知变量x,y满足约束条件
,则z=x+2y的最大值为( )
|
| A、6 | B、5 | C、4 | D、3 |
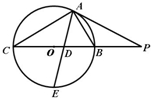 如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E. 如图,已知△ABC内接于圆O,点D在OC的延长线上,AD是⊙O的切线,若∠B=30°,AC=3,则OD的长为
如图,已知△ABC内接于圆O,点D在OC的延长线上,AD是⊙O的切线,若∠B=30°,AC=3,则OD的长为