题目内容
在区域D:(x-1)2+y2≤4内随机取一个点,则此点到点A(1,2)的距离大于2的概率是 .
考点:几何概型
专题:概率与统计
分析:确定满足到点A(1,2)的距离小于2的点的区域,求出其面积,以面积为测度可求概率.
解答:
 解:区域D:(x-1)2+y2≤4的面积为4π,满足到点A(1,2)的距离小于2的点在如图的区域内.
解:区域D:(x-1)2+y2≤4的面积为4π,满足到点A(1,2)的距离小于2的点在如图的区域内.
由题意,∠ACB=120°,∴S阴影=2(
π•22-
•2•2•sin120°)=
-2
,
∴在区域D:(x-1)2+y2≤4内随机取一个点,此点到点A(1,2)的距离大于2的概率是
=
+
.
故答案为:
+
.
 解:区域D:(x-1)2+y2≤4的面积为4π,满足到点A(1,2)的距离小于2的点在如图的区域内.
解:区域D:(x-1)2+y2≤4的面积为4π,满足到点A(1,2)的距离小于2的点在如图的区域内.由题意,∠ACB=120°,∴S阴影=2(
| 1 |
| 3 |
| 1 |
| 2 |
| 8π |
| 3 |
| 3 |
∴在区域D:(x-1)2+y2≤4内随机取一个点,此点到点A(1,2)的距离大于2的概率是
4π-(
| ||||
| 4π |
| 1 |
| 3 |
| ||
| 2π |
故答案为:
| 1 |
| 3 |
| ||
| 2π |
点评:本题考查概率的计算,考查图形面积的计算,确定图形的面积是关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
一个几何体的三视图如图所示,这个几何体可能是一个( )
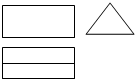

| A、三棱锥 |
| B、底面不规则的四棱锥 |
| C、三棱柱 |
| D、底面为正方形的四棱锥 |
已知集合A={x||x|<3},B={x|x-2≤0},则A∪B等( )
| A、(-∞,3] |
| B、(-∞,3) |
| C、[2,3) |
| D、(-3,2] |
某几何体的三视图如图所示,则它的表面积为( )


A、2+
| ||||
B、2+
| ||||
C、2+(1+
| ||||
D、2+
|
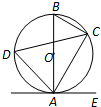 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.