题目内容
已知椭圆
+
=1上一点P到一个焦点的距离为8，则点P到另一焦点的距离是 ．
| x2 |
| 100 |
| y2 |
| 64 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由椭圆方程找出a的值，根据椭圆的定义可知椭圆上的点到两焦点的距离之和为常数2a，把a的值代入即可求出常数的值得到P到两焦点的距离之和，由P到一个焦点的距离为8，求出P到另一焦点的距离即可．
解答：
解：由椭圆
+
=1，得a=10，
则2a=20，且点P到椭圆一焦点的距离为8，
由定义得点P到另一焦点的距离为2a-8=20-8=12．
故答案为：12．
| x2 |
| 100 |
| y2 |
| 64 |
则2a=20，且点P到椭圆一焦点的距离为8，
由定义得点P到另一焦点的距离为2a-8=20-8=12．
故答案为：12．
点评：此题考查学生掌握椭圆的定义及简单的性质，是一道中档题．
练习册系列答案
名校课堂系列答案
相关题目
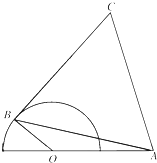如图，半圆O的直径为2，A为直径延长线上的一点，OA=2，B为半圆上任意一点，以AB为一边作等边三角形ABC．