题目内容
6.在以下的类比推理中结论正确的是( )| A. | 若a•3=b•3,则a=b类比推出 若a•0=b•0,则a=b | |
| B. | 若(a+b)c=ac+bc类比推出 $\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}$(c≠0) | |
| C. | 若(a+b)c=ac+bc类比推出 (a•b)c=ac•bc | |
| D. | 若(ab)n=anbn类比推出 (a+b)n=an+bn |
分析 根据等式的基本性质,可以分析①中结论的真假;
根据等式的基本性质,可以分析②中结论的真假;
根据指数的运算性质,可以分析③中结论的真假;
根据对数的运算性质,可以分析④中结论的真假.
解答 解:A中“若a•3=b•3,则a=b”类推出“若a•0=b•0,则a=b”,结论不正确;
B中“若(a+b)c=ac+bc类比推出 $\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}$(c≠0)结论正确;
C中若(a+b)c=ac+bc”类比出“(a•b)c=ac•bc”,结论不正确;
D中“(ab)n=anbn”类推出“(a+b)n=an+bn”,结论不正确.
故选:B.
点评 本题考查类比推理,其中熟练掌握各种运算性质,是解答本题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
14.设f,g都是由A到A的映射,其对应法则如表(从上到下);
表1 映射f对应法则
表2 映射g的对应法则
则与f[g(1)]相同的是( )
表1 映射f对应法则
| 原像 | 1 | 2 | 3 | 4 |
| 像 | 3 | 4 | 2 | 1 |
| 原像 | 1 | 2 | 3 |
| 像 | 4 | 3 | 1 |
| A. | g[f(3)] | B. | g[f(2)] | C. | g[f(4)] | D. | g[f(1)] |
11.在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据完成下面的2×2列联表;
(2)判断性别与休闲方式是否有关系.
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
(1)根据以上数据完成下面的2×2列联表;
(2)判断性别与休闲方式是否有关系.
| 休闲方式 性别 | 看电视 | 运动 | 总计 |
| 女 | 43 | 27 | 70 |
| 男 | 21 | 33 | 54 |
| 总计 | 64 | 60 | 124 |
| P(K2≥k ) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
18.某几何体的三视图如图所示,则该几何体的体积为( )
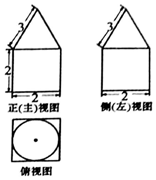

| A. | 4+2$\sqrt{2}$π | B. | 8+2$\sqrt{2}$π | C. | 4+$\frac{2\sqrt{2}}{3}$π | D. | 8+$\frac{2\sqrt{2}}{3}$π |