题目内容
1.已知函数f(x)对一切实数x,y都有f(x+y)-f(y)=x(x+2y+1)成立,且f(1)=0.(1)求f(0)的值;
(2)求f(x)的解析式;
(3)已知a,b∈R,当$0<x<\frac{1}{2}$时,不等式f(x)+3<2x+a恒成立的a的集合记为A;当x∈[-2,2]时,使g(x)=f(x)-bx是单调函数的b的集合记为B.求A∩∁RB(R为全集).
分析 (1)令x=-1,y=1,利用f(x+y)-f(y)=x(x+2y+1),即可求得f(0)的值;
(2)令y=0,则f(x)-f(0)=x(x+1),结合f(0)=-2,可求f(x)的解析式;
(3)根据题意,将f(x)+3<2x+a变形可得x2-x+1<a,分析x2-x+1的最大值,可得a的范围,即集合A;由(2)可得g(x)的解析式,结合二次函数的性质可得b的取值范围,即可得集合B,进而可得CRB;从而可求A∩CRB.
解答 解:(1)根据题意,在f(x+y)-f(y)=x(x+2y+1)中,
令x=-1,y=1,可得f(0)-f(1)=-1(-1+2+1),
又由f(1)=0,则有f(0)=-2;
(2)在f(x+y)-f(y)=x(x+2y+1)中,
令y=0,则f(x)-f(0)=x(x+1)
又由f(0)=-2,则f(x)=x2+x-2;
(3)不等式f(x)+3<2x+a,等价于x2+x-2+3<2x+a,即x2-x+1<a,
若不等式f(x)+3<2x+a恒成立,则有x2-x+1<a恒成立,
又由$0<x<\frac{1}{2}$,则$\frac{3}{4}$<x2-x+1<1,必有a>1;
故A={a|a≥1};
g(x)=x2+x-2-ax=x2+(1-a)x-2,
若g(x)在[-2,2]上是单调函数,必有$\frac{a-1}{2}$≤-2或$\frac{a-1}{2}$≥2成立,
解可得a≤-3,或a≥5.
故B={a|a≤-3,或a≥5},则CRB={a|-3<a<5}
故A∩CRB={a|1≤a<5}.
点评 本题考查抽象函数的运用,涉及二次函数的性质,此类问题一般用特殊值法分析,解题的关键是利用二次函数的性质化简集合A,B.

练习册系列答案
相关题目
6.在以下的类比推理中结论正确的是( )
| A. | 若a•3=b•3,则a=b类比推出 若a•0=b•0,则a=b | |
| B. | 若(a+b)c=ac+bc类比推出 $\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}$(c≠0) | |
| C. | 若(a+b)c=ac+bc类比推出 (a•b)c=ac•bc | |
| D. | 若(ab)n=anbn类比推出 (a+b)n=an+bn |
13.将函数f(x)=sin2x+$\sqrt{3}$cos2x图象上所有点向右平移$\frac{π}{6}$个单位长度,得到函数g (x)的图象,则g(x)图象的一个对称中心是( )
| A. | ($\frac{π}{3}$,0) | B. | ( $\frac{π}{4}$,0) | C. | (-$\frac{π}{12}$,0) | D. | ($\frac{π}{2}$,0) |
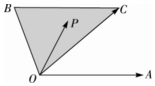 已知图中∠AOC+2∠BOC=π,|$\overrightarrow{OA}$|=|$\overrightarrow{OC}$|,BC∥OA,P为图中的阴影中(含边界)任意点,并且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OC}$,下列正确的是①③⑤
已知图中∠AOC+2∠BOC=π,|$\overrightarrow{OA}$|=|$\overrightarrow{OC}$|,BC∥OA,P为图中的阴影中(含边界)任意点,并且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OC}$,下列正确的是①③⑤