题目内容
有下列关于三角函数的命题
P1:?x∈R,x≠kπ+
(k∈Z),若tanx>0,则sin2x>0;
P2:函数y=sin(x-
)与函数y=cosx的图象相同;
P3:?x0∈R,2cosx0=3;
P4:函数y=|cosx|(x∈R)的最小正周期为2π,其中真命题是( )
P1:?x∈R,x≠kπ+
| π |
| 2 |
P2:函数y=sin(x-
| 3π |
| 2 |
P3:?x0∈R,2cosx0=3;
P4:函数y=|cosx|(x∈R)的最小正周期为2π,其中真命题是( )
| A、P1,P4 |
| B、P2,P4 |
| C、P2,P3 |
| D、P1,P2 |
考点:命题的真假判断与应用
专题:阅读型,三角函数的图像与性质,简易逻辑
分析:运用二倍角的正弦公式和同角的平方关系以及商数关系,即可化简判断P1;运用三角函数的诱导公式化简,即可判断P2;由余弦函数的值域,即可判断P3;运用周期函数的定义,结合诱导公式,即可判断P4.
解答:
解:对于P1,?x∈R,x≠kπ+
(k∈Z),若tanx>0,则sin2x=2sinxcosx
=
=
>0,则P1为真命题;
对于P2,函数y=sin(x-
)=sin(2π+x-
)=sin(x+
)=cosx,则P2为真命题;
对于P3,由于cosx∈[-1,1],
∉[-1,1],则P3为假命题;
对于P4,函数y=|cosx|(x∈R),f(x+π)=|cos(x+π)|=|-cosx|=|cosx|=f(x),
则f(x)的最小正周期为π,则P4为假命题.
故选D.
| π |
| 2 |
=
| 2sinxcosx |
| sin2x+cos2x |
| 2tanx |
| 1+tan2x |
对于P2,函数y=sin(x-
| 3π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
对于P3,由于cosx∈[-1,1],
| 3 |
| 2 |
对于P4,函数y=|cosx|(x∈R),f(x+π)=|cos(x+π)|=|-cosx|=|cosx|=f(x),
则f(x)的最小正周期为π,则P4为假命题.
故选D.
点评:本题考查全称性命题和存在性命题的真假,以及三角函数的图象和周期,运用二倍角公式和诱导公式以及周期函数的定义是解题的关键,属于基础题和易错题.

练习册系列答案
相关题目
如图1所示,长方体AC1沿截面A1C1MN截得几何体DMN-D1A1C1,它的正视图、侧视图均为图2所示的直角梯形,则该几何体的体积为( )
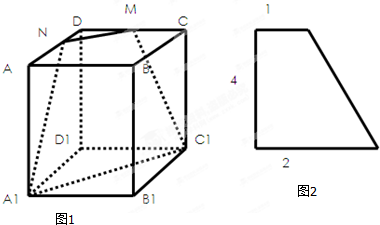

A、
| ||
B、
| ||
| C、14 | ||
| D、10 |
对一切实数x,不等式ax2-ax-2<0恒成立,则实数a的取值范围是( )
| A、[-8,0] |
| B、(-8,0) |
| C、(-8,0] |
| D、[0,8) |
抛物线C1:x2=2y的焦点为F,以F为圆心C2交C1于A,B两点,交C1准线于C,D两点,若四边形ABCD是矩形,则C2的标准方程为( )
A、x2+(y-
| ||
B、(x-
| ||
C、x2+(y-
| ||
D、(x-
|
如图所示程序框图,其功能是输入x的值,输出相应的y值,若要使输入的x值与输出的y值相等,则这样的x值有( )


| A、2个 | B、3个 | C、4个 | D、5个 |
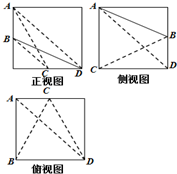 在棱长为2的正方体内有一四面体A-BCD,其中B,C分别为正方体两条棱的中点,其三视图如图所示,则四面体A-BCD的体积为( )
在棱长为2的正方体内有一四面体A-BCD,其中B,C分别为正方体两条棱的中点,其三视图如图所示,则四面体A-BCD的体积为( )