题目内容
已知在Rt△ABC中,其中∠A为直角,向量
=
+
,
=2
+3
,
=(2m+1)
+(m-3)
,其中
,
是互相垂直的两个单位向量.
(1)求实数m的值;
(2)过A作AE⊥BC于E,延长AE至D,使四边形ABDC为直角梯形(其中AC、BD为底边),用
,
表示
.
| OA |
| i |
| j |
| OB |
| i |
| j |
| OC |
| i |
| j |
| i |
| j |
(1)求实数m的值;
(2)过A作AE⊥BC于E,延长AE至D,使四边形ABDC为直角梯形(其中AC、BD为底边),用
| i |
| j |
| OD |
考点:平面向量数量积的运算,向量加减混合运算及其几何意义
专题:平面向量及应用
分析:(1)以
,
为直角坐标系的单位向量建立直角坐标系.此时
=(1,1),
=(2,3),
=(2m+1,m-3),可得
,
.由∠A为直角,可得
•
=0,解得m即可.
(2)设
=(x,y),
=(x-2,y-3),
=(4,-2),利用
∥
,可得x+2y-8=0.又
=(x-1,y-1),
=(3,-4),利用
⊥
,可得
•
=0,3x-4y+1=0,联立解出即可.
| i |
| j |
| OA |
| OB |
| OC |
| AB |
| AC |
| AB |
| AC |
(2)设
| OD |
| BD |
| AC |
| AC |
| BD |
| AD |
| BC |
| AD |
| BC |
| AD |
| BC |
解答:
解:(1)以
,
为直角坐标系的单位向量建立直角坐标系.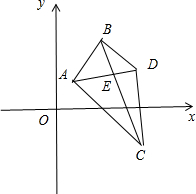
此时
=(1,1),
=(2,3),
=(2m+1,m-3),
=(1,2),
=(2m,m-4).
∵∠A为直角,
∴
•
=2m+2(m-4)=0,解得m=2.
(2)设
=(x,y),
=(x-2,y-3),
=(4,-2),
∵
∥
,∴-2(x-2)=4(y-2),即x+2y-8=0.
又
=(x-1,y-1),
=(3,-4),
∵
⊥
,可得3(x-1)-4(y-1)=0,化为3x-4y+1=0,
联立
,解得
,
∴
=(3,
),即
=3
+
.
| i |
| j |

此时
| OA |
| OB |
| OC |
| AB |
| AC |
∵∠A为直角,
∴
| AB |
| AC |
(2)设
| OD |
| BD |
| AC |
∵
| AC |
| BD |
又
| AD |
| BC |
∵
| AD |
| BC |
联立
|
|
∴
| OD |
| 5 |
| 2 |
| OD |
| i |
| 5 |
| 2 |
| j |
点评:本题考查了向量共线定理、向量垂直与数量积的关系、直角梯形的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知某几何体的三视图如图所示,则该几何体的体积等于( )
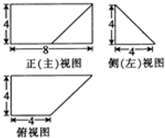

A、
| ||
| B、160 | ||
C、64+32
| ||
| D、60 |
如图1所示,长方体AC1沿截面A1C1MN截得几何体DMN-D1A1C1,它的正视图、侧视图均为图2所示的直角梯形,则该几何体的体积为( )
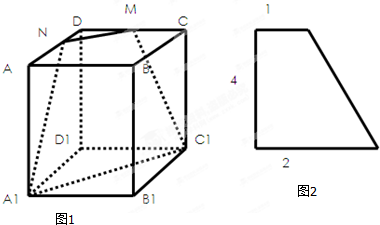

A、
| ||
B、
| ||
| C、14 | ||
| D、10 |
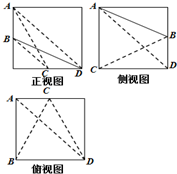 在棱长为2的正方体内有一四面体A-BCD,其中B,C分别为正方体两条棱的中点,其三视图如图所示,则四面体A-BCD的体积为( )
在棱长为2的正方体内有一四面体A-BCD,其中B,C分别为正方体两条棱的中点,其三视图如图所示,则四面体A-BCD的体积为( )